Question

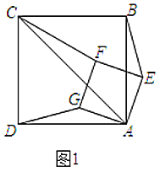
【题目】如图，在每个小正方形的边长为1的网格中，，，为格点，为小正方形边的中点.

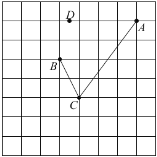
（1）的长等于_________；

（2）点，分别为线段，上的动点，当取得最小值时，请在如图所示的网格中，用无刻度的直尺，画出线段，，并简要说明点和点的位置是如何找到的（不要求证明）.

Answer 1

【答案】（1）5；（2）见解析

【解析】

（1）直接利用勾股定理计算可得；

（2）令BC与网格交于P，再分别取网格线中点G和H，连接，与AC交于Q，从而可得.

解：（1）由图可得：

AC=，

故答案为：5；

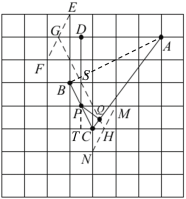
（2）如图，与网格线相交，得点；取格点，，连接，与网格线相交，得点，取格点，，连接，与网格线相交，得点，连接，与相交，得点.连接，.线段，即为所求.

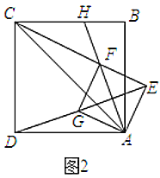
如图，延长DP，交网格线于点T，连接AB，GH与DP交于点S，

由计算可得：AB=，BC=，AC=5，

∴△ABC为直角三角形，∠ABC=90°，

∴tan∠ACB=2，

∵tan∠BCT=PT：TC=2，

∴∠ACB=∠BCT，即BC平分∠ACT，

根据画图可知：GH∥BC，

∴∠ACB=∠CQH，∠BCT=∠GHC，

∵∠BCT=∠BCA，

∴∠CQH=∠GHC，

∴CQ=CH，

由题意可得：BS=CH，

∴BS=CQ，

又∵BP=CP，∠PBS=∠PCQ，

∴△BPS≌△CPQ，

∴∠PSB=∠PHC=90°，即PQ⊥AC，

∴PD+PQ的最小值即为PD+PT，

∴所画图形符合要求.