题目内容
【题目】问题情境:
我们知道若一个矩形的周长固定,当相邻两边相等,即为正方形时,面积是最大的,反过来,若一个矩形的面积固定,它的周长是否会有最值呢?
方法探究:
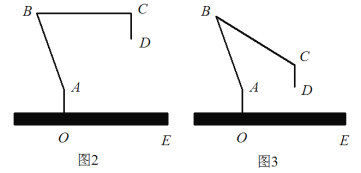
用两条直角边分别为![]() 、
、![]() 的四个全等的直角三角形,可以拼成一个正方形,
的四个全等的直角三角形,可以拼成一个正方形,
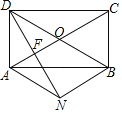
若![]() ,可以拼成如图1的正方形,从而得到
,可以拼成如图1的正方形,从而得到![]() ,即
,即![]() ;
;
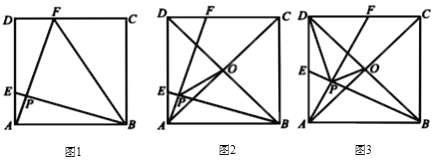
若![]() ,可以拼成如图2的正方形,从而得到
,可以拼成如图2的正方形,从而得到![]() ,即
,即![]() .
.
于是我们可以得到结论:![]() ,
,![]() 为正数,总有
为正数,总有![]() ,且当
,且当![]() 时,代数式
时,代数式![]() 取得最小值为
取得最小值为![]() .
.
另外,我们也可以通过代数式运算得到类似上面的结论.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴对于任意实数![]() ,
,![]() ,总有
,总有![]() ,
,
且当![]() 时,代数式
时,代数式![]() 取得最小值为
取得最小值为![]() .
.
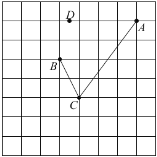
类比应用:
(1)对于正数![]() ,
,![]() ,试比较
,试比较![]() 和
和![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
(2)填空:
当![]() 时,
时,![]() ________.
________.
代数式![]() 有最________值为________.
有最________值为________.
问题解决:
(3)若一个矩形的面积固定为![]() ,它的周长是否会有最值呢?若有,求出周长的最值,及此时矩形的长和宽;若没有,请说明理由.
,它的周长是否会有最值呢?若有,求出周长的最值,及此时矩形的长和宽;若没有,请说明理由.
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;小;
;小;![]() ;(3)若一个矩形的面积固定为
;(3)若一个矩形的面积固定为![]() ,它的周长是有最小值,周长的最小值为
,它的周长是有最小值,周长的最小值为![]() ,矩形的长和宽均为
,矩形的长和宽均为![]()
【解析】
(1)根据探究方法中的结论,代入数据即得出结论;
(2)先将代数式-2,再+2,根据探究方法中的结论,代入数据即得出结论;
(3)设该矩形的长为![]() ,宽为
,宽为![]()
![]() ,根据
,根据![]() ,结合矩形的周长和面积公式即可得出结论.
,结合矩形的周长和面积公式即可得出结论.
探究方法:
(1)解:∵当![]() ,
,![]() 均为正数时,
均为正数时,
∵![]()
∴![]() ,
,
∴![]() .
.
类比应用:
(2)结合探究方法中得出的结论可知:
当![]() 时,
时,![]() ,代数式
,代数式![]() 有最小值为
有最小值为![]() .
.
(3)问题解决:
解:设该矩形的长为![]() ,宽为
,宽为![]()
![]() ,
,
根据题意知:周长![]() ,
,
且当![]() 时,代数式
时,代数式![]() 取得最小值为
取得最小值为![]() ,
,
此时![]() .
.
故若一个矩形的面积固定为![]() ,它的周长是有最小值,周长的最小值为
,它的周长是有最小值,周长的最小值为![]() ,此时矩形的长和宽均为
,此时矩形的长和宽均为![]() .
.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛赛,后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列统计图表:
取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩 |
|
|
|
|
|
|
|
|
|
|
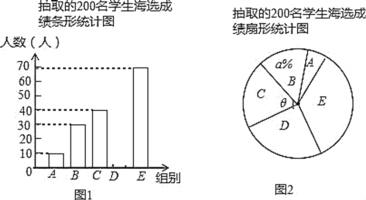
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整,在条形图![]() 的顶端标示对应的人数;
的顶端标示对应的人数;
(2)直接写明在图2的扇形统计图中,表示![]() 组扇形的圆心角
组扇形的圆心角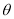 的度数为________度;
的度数为________度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请根据样本,求:该校参加这次海选比赛的2000名学生中,成绩“优等”的有多少人?