题目内容
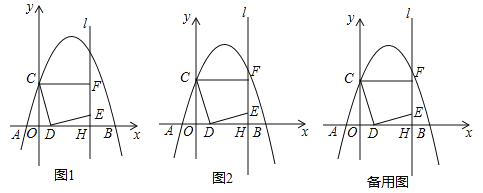
【题目】在矩形![]() 中,
中,![]() 为
为![]() 的中点,一块足够大的三角板的直角顶点与点
的中点,一块足够大的三角板的直角顶点与点![]() 重合,将三角板绕点
重合,将三角板绕点![]() 旋转,三角板的两直角边分别交
旋转,三角板的两直角边分别交![]() 或它们的延长线)于点
或它们的延长线)于点![]() ,设
,设![]() ,下列四个结论:①
,下列四个结论:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
过点G作GH⊥BC于H,可证四边形ABHG是矩形,可得AB=GH=1,AG=BH=1,∠AGH=90°=∠EGF,由“ASA”可证△AEG≌△HFG,可得AE=HF,GE=GF,∠AEG=∠BFG,即可判断②;由旋转的性质可得点F的位置不确定,可判断①③;由锐角三角函数可得GE=![]() =
=![]() ,可求出△GEF的面积,可判断④,即可求解.
,可求出△GEF的面积,可判断④,即可求解.
解:如图,过点G作GH⊥BC于H,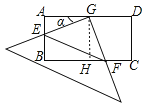
∵在矩形ABCD中,AD=2,AB=1,G为AD的中点,
∴∠A=∠B=90°,AG=DG=1=AB,
又∵GH⊥BC,
∴四边形ABHG是矩形,
∴AB=GH=1,AG=BH=1,∠AGH=90°=∠EGF,
∴∠AGE=∠FGH,
又∵∠A=∠GHF=90°,AG=GH=1,
∴△AEG≌△HFG(ASA)
∴AE=HF,GE=GF,∠AEG=∠BFG,故②正确,
∵将三角板绕点G旋转,三角板的两直角边分别交AB、BC(或它们的延长线)于点E、F,
∴点F的位置不确定,
∴HF不一定等于CF,
∴AE不一定等于CF,故①不正确,
若点F在线段CH上时,CH=HF+CF=AE+CF=1,
若点F在HC的延长线上时,CH=HF-CF=AE-CF=1,
故③不正确,
在Rt△AEG中,GE=![]() =
=![]() ,
,
∵GE=GF,∠EGF=90°,
∴S△EFG=![]() EG2=
EG2=![]() ×
×![]() .
.
故④不正确,
故选:A.

【题目】阅读对学生的成长有着深远的影响.某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调查结果经制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合计 | 1 |
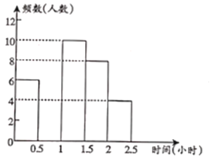
请根据图表中的信息,解答下列问题:
(1)表中的![]() ,
,![]() ,将频数分布直方图补全;
,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足1小时的学生大约有多少名?
(3)![]() 组的4人中,有1名男生和3名女生,该校计划在
组的4人中,有1名男生和3名女生,该校计划在![]() 组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.