题目内容
6.某中学为了解学生上学方式,现随机抽取部分学生进行调查,将调查结果绘成如图所示的条形图、扇形图,根据图中信息回答:(1)这次共调查100名学生;
(2)图中m=25;
(3)a区域所对的圆心角度数是46.8°;
(4)若该中学有2400名学生,根据以上信息估计有600名学生进行上学.
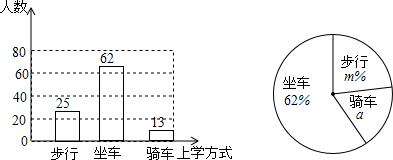
分析 (1)利用调查的学生数=坐车的人数÷对应的百分比求解即可,
(2)利用步行人数的百分比=步行人数÷调查总人数求解即可,
(3)利用a区域所对的圆心角度数=360°×a区域的百分比求解即可,
(4)利用总人数×步行人数的百分比求解即可.
解答 解:(1)这次共调查的学生数为:62÷62%=100(名).
故答案为:100.
(2)步行人数的百分比为:$\frac{25}{100}$=25%,
所以m=25.
故答案为:25.
(3)a区域所对的圆心角度数是360°×(1-25%-62%)=46.8°,
故答案为:46.8°.
(4)2400×25%=600(人)
答:步行上学的有600人.
故答案为:600.
点评 本题考查了条形统计图和扇形统计图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
1.在△ABC中,已知cosB=$\frac{3}{5}$,sinC=$\frac{2}{3}$,AC=2,那么边AB等于( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{20}{9}$ | D. | $\frac{12}{5}$ |
11.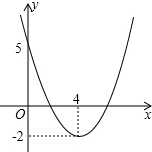 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )| A. | m≥-2 | B. | m≥5 | C. | m≥0 | D. | m>4 |
16.下列运算中错误的是( )
| A. | $\frac{a}{b}$=$\frac{a{c}^{2}}{b{c}^{2}}$ | B. | $\frac{-a-b}{a+b}$=-1 | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a}{b}$=$\frac{a({k}^{2}+1)}{b({k}^{2}+1)}$ |
 已知一次函数的图象经过点A(1,2)和点B(-3,-2).
已知一次函数的图象经过点A(1,2)和点B(-3,-2). 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑至B.已知AB=200m,这名滑雪运动员的高度下降了100m.
如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑至B.已知AB=200m,这名滑雪运动员的高度下降了100m.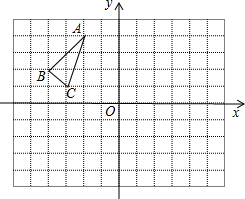 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图: