题目内容
6.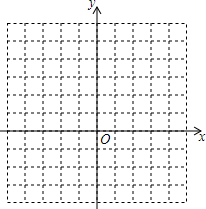 已知二次函数的解析式是y=x2-2x-3.
已知二次函数的解析式是y=x2-2x-3.(1)与x轴的交点坐标是(-1,0),(3,0),顶点坐标是(1,-4);
(2)在坐标系中利用描点法画出此抛物线;
| x | … | … | |||||
| y | … | … |
分析 (1)根据抛物线y=x2-2x-3,可以求得抛物线与x轴和y轴的交点;
(2)根据第一问中的三个坐标和二次函数图象具有对称性,在表格中填入合适的数据,然后再描点作图即可;
(3)根据第二问中的函数图象结合对称轴可以直接写出答案.
解答 解:(1)令y=0,则0=x2-2x-3.
解得x1=-1,x2=3.
抛物线y=x2-2x-3与x轴交点的坐标为(-1,0),(3,0).
y=x2-2x-3=(x-1)x2-4,
所以它的顶点坐标为(1,-4);
(2)列表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | 0 | … |
 ;
;(3)当-2<x<1时,-4<y<5;
当1<x<2时,-4<y<-3.
点评 本题考查二次函数的图象与性质,二次函数与x轴、y轴的交点、求顶点坐标,画二次函数的图象,关键是可以根据图象得出所求问题的答案.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
17.在-8,2.6,-3$\frac{1}{2}$,2$\frac{2}{3}$,-5.7中,负分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
11.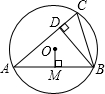 如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
 如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A. | OM的长 | B. | $\frac{1}{2}$OM的长 | C. | 2OM的长 | D. | CD的长 |
15.下列长度的各组线段,能组成直角三角形的是( )
| A. | 12,15,18 | B. | 12,35,36 | C. | 0.3,0.4,0.5 | D. | 2,3,4 |
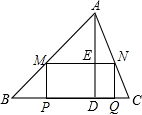 在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.
在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y. 如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.若AB=2DE,∠E=18°,则∠C的度数为36°.
如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.若AB=2DE,∠E=18°,则∠C的度数为36°.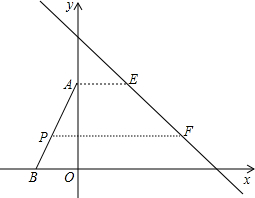 如图,△ABO的顶点A、B的坐标分别为(0,4)、(-2,0),直线l交x轴于C、交y轴于D,且它所对应的函数表达式为y=-x+6;规定:对于平面上的某一点M,当它沿水平向右的方向平移,平移到直线l上为止,这个过程中平移的距离,称为点M的“右平移距离”.
如图,△ABO的顶点A、B的坐标分别为(0,4)、(-2,0),直线l交x轴于C、交y轴于D,且它所对应的函数表达式为y=-x+6;规定:对于平面上的某一点M,当它沿水平向右的方向平移,平移到直线l上为止,这个过程中平移的距离,称为点M的“右平移距离”.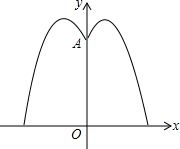 某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子0A,0恰在水面中心,安装在柱子顶端A处的两个旋转喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过0A的任意平面上,抛物线形状如图所示,建立平面直角坐标系,右边-条抛物线水流喷出的高度y(m)与水面距离x(m)之间的关系式是y=-x2+2x+$\frac{7}{2}$.请回答下列问题:
某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子0A,0恰在水面中心,安装在柱子顶端A处的两个旋转喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过0A的任意平面上,抛物线形状如图所示,建立平面直角坐标系,右边-条抛物线水流喷出的高度y(m)与水面距离x(m)之间的关系式是y=-x2+2x+$\frac{7}{2}$.请回答下列问题: