题目内容
14. 如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.若AB=2DE,∠E=18°,则∠C的度数为36°.
如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.若AB=2DE,∠E=18°,则∠C的度数为36°.
分析 根据AB=2DE得DE等于圆的半径,在△EDO和△CEO中,根据三角形的一个外角等于和它不相邻的两个内角的和求解.
解答  解:连接OD,∵AB=2DE,
解:连接OD,∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD,
在△EDO中,∠ODC=∠E+∠EOD=36°,
∵OC=OD,
∴∠C=∠ODC=36°.
故答案为:36°.
点评 本题主要考查了三角形的外角和定理,外角等于不相邻的两个内角的和.

练习册系列答案
相关题目
5.下列分式$\frac{1}{{(x-1{)^2}}}$,$\frac{1}{{{x^2}+1}}$,$\frac{5}{x-1}$的最简公分母为( )
| A. | (x2+1)(x-1) | B. | (x-1)2 | C. | (x-1)2(x2+1) | D. | (x2-1)(x2+1) |
9.计算$\sqrt{16}$的平方根结果是( )
| A. | ±2 | B. | ±4 | C. | 2 | D. | 4 |
6.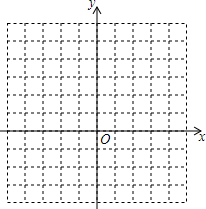 已知二次函数的解析式是y=x2-2x-3.
已知二次函数的解析式是y=x2-2x-3.
(1)与x轴的交点坐标是(-1,0),(3,0),顶点坐标是(1,-4);
(2)在坐标系中利用描点法画出此抛物线;
(3)结合图象回答:当-2<x<2时,函数值y的取值范围是当-2<x<1时,-4<y<5;当1<x<2时,-4<y<-3.
 已知二次函数的解析式是y=x2-2x-3.
已知二次函数的解析式是y=x2-2x-3.(1)与x轴的交点坐标是(-1,0),(3,0),顶点坐标是(1,-4);
(2)在坐标系中利用描点法画出此抛物线;
| x | … | … | |||||
| y | … | … |
4.计算x2y3÷(xy)-2的结果为( )
| A. | xy | B. | x | C. | x4y5 | D. | y |
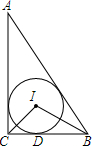 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求: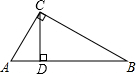 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=3,BD=8,则CD=2$\sqrt{6}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=3,BD=8,则CD=2$\sqrt{6}$.