题目内容
18.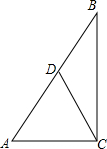 已知:如图,在△ABC中,点D是AB边的中点,且CD=$\frac{1}{2}$AB,求证:∠ACB=90°.
已知:如图,在△ABC中,点D是AB边的中点,且CD=$\frac{1}{2}$AB,求证:∠ACB=90°.
分析 先由CD=$\frac{1}{2}$AB,得到AD=CD,根据等边对等角得出∠ACD=∠A,再由中点的定义得到AD=BD,则BD=CD,∠BCD=∠B,然后在△ABC中,根据三角形内角和定理得出∠A+∠B+(∠ACD+∠BCD)=180°,即可证明∠ACD+∠BCD=90°,即∠ACB=90°.
解答 证明:∵点D是AB边的中点,且CD=$\frac{1}{2}$AB,
∴AD=CD,
∴∠ACD=∠A.
∵点D为△ABC的边AB的中点,
∴AD=BD,
∵AD=CD,
∴BD=CD,
∴∠BCD=∠B.
∵∠A+∠B+(∠ACD+∠BCD)=180°,
∴∠ACD+∠BCD+(∠ACD+∠BCD)=180°,
∴2(∠ACD+∠BCD)=180°,
∴∠ACD+∠BCD=90°,
即∠ACB=90°.
点评 本题考查了等腰三角形等边对等角的性质,中点的定义,三角形内角和定理,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
6.已知a2-ab=20,ab-b2=-12,则a2-b2和a2-2ab+b2的值分别为( )
| A. | -8和32 | B. | 8和32 | C. | -32和32 | D. | 8和-32 |
 如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,求证:AO⊥BC.
如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,求证:AO⊥BC. 如图,∠A0B内有-点P,在0A、0B上分别找点M、N,使△PMN的周长最小.
如图,∠A0B内有-点P,在0A、0B上分别找点M、N,使△PMN的周长最小.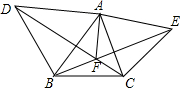 分别以△ABC的AB、AC为边向外作等边△ABD和等边△ACE,连结CD、BE交于F,求证:AF平分∠DFE.
分别以△ABC的AB、AC为边向外作等边△ABD和等边△ACE,连结CD、BE交于F,求证:AF平分∠DFE.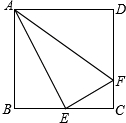 如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.
如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.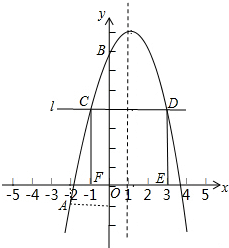 如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.
如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.