题目内容
8.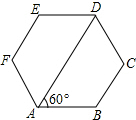 如图,六边形ABCDEF的内角都相等,∠DAB=60°.求证:AB∥ED,BC∥EF.
如图,六边形ABCDEF的内角都相等,∠DAB=60°.求证:AB∥ED,BC∥EF.
分析 首先求得多边形的各个角的度数,然后根据平行线的判定定理以及性质定理即可得出结论.
解答 证明:∵六边形ABCDEF的内角都相等,
∴∠FAB=∠B=∠C=∠CDE=∠E=∠F=120°,
又∵∠DAB=60°,
∴∠FAD=∠DAB=60°,
∴∠F+∠FAD=∠B+∠DAB=180°,
∴BC∥AD,EF∥AD,
∴BC∥EF.
∵BC∥AD,∠C=120°,
∴∠C+∠ADC=180°,
又∵∠C=120°,
∴∠ADC=60°,
∴∠EDA=60°,
∴∠EDA=∠DAB,
∴AB∥DE.
点评 本题考查多边形的内角的计算以及平行线的判定与性质定理,理解定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.⊙O的半径为6,圆心O的坐标为(0,0),点P的坐标为(3,4),则点P与⊙O的位置关系是( )
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 不能确定 |
16.数字解密:第一个数是3=2-(-1),第二个数是5=3-(-2),第三个数是9=5-(-4),第四个数是17=9-(-8),…,则第六个数是( )
| A. | 33=17-(-16) | B. | 65=33-(-32) | C. | 129=65-(-64) | D. | 55=28-(-27) |
3.如果一元一次方程3x-b=0的根x=2,那么一次函数y=3x-b的图象一定过点( )
| A. | (0,2) | B. | (2,0) | C. | (-2,0) | D. | (0,-2) |