题目内容
13.通分:(1)$\frac{1}{4{x}^{2}-xy}$,$\frac{x}{{y}^{2}-4xy}$;
(2)$\frac{1}{{x}^{2}-4x+4}$,$\frac{x}{{x}^{2}-4}$.
分析 (1)根据提取公因式可分解4x2-xy与y2-4xy,再找系数的最小公倍数,字母的最高次幂,即可得出最简公分母;
(2)根据完全平方公式分解x2-4x+4,再利用平方差公式分解x2-4,再找系数的最小公倍数,字母的最高次幂,即可得出最简公分母.
解答 解:(1)∵4x2-xy=x(4x-y),y2-4xy=y(y-4x)=-y(4x-y),
∴分式$\frac{1}{4{x}^{2}-xy}$,$\frac{x}{{y}^{2}-4xy}$的最简公分母为-xy(4x-y);
(2)∵x2-4x+4=(x-2)2,x2-4=(x+2)(x-2),
∴分式$\frac{1}{{x}^{2}-4x+4}$,$\frac{x}{{x}^{2}-4}$的最简公分母为(x-2)2(x+2).
点评 本题考查了分式的通分,通分的关键是分解各个分母,找出最简公分母.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
3. 如图所示几何体的几何体的主视图是( )
如图所示几何体的几何体的主视图是( )
 如图所示几何体的几何体的主视图是( )
如图所示几何体的几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
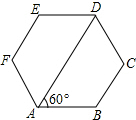 如图,六边形ABCDEF的内角都相等,∠DAB=60°.求证:AB∥ED,BC∥EF.
如图,六边形ABCDEF的内角都相等,∠DAB=60°.求证:AB∥ED,BC∥EF. 如图所示,△ABC中,D点在AC上,E点在BC上,且满足△ABD≌△EBD,△DBE≌△DCE,求∠A和∠C的度数.
如图所示,△ABC中,D点在AC上,E点在BC上,且满足△ABD≌△EBD,△DBE≌△DCE,求∠A和∠C的度数.