题目内容
20.解方程:|x+1|+|x-1|=2.分析 分别讨论①x≤-1,②-1<x≤1,③x>1,根据x的范围去掉绝对值,解出x,综合三种情况可得出x的最终范围.
解答 解:当x≤-1时,原式即-x-1+1-x=2,
即-2x=1,
解得x=-1;
当-1<x≤1时,原式即x+1+1-x=2,一定成立;
当x>1时,原式即x+1+x-1=2,
解得:x=1(舍去).
总之,当-1≤x≤1的任意数都是方程的解.
点评 本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键,意最后的解可以联合起来,难度很大.

练习册系列答案
相关题目
8.若($\frac{4}{{a}^{2}-4}$+$\frac{1}{2-a}$)•w=1,则w=( )
| A. | a+2(a≠-2) | B. | -a+2(a≠2) | C. | a-2(a≠2) | D. | -a-2(a≠-2) |
12.下列计算结果中是负数的是( )
| A. | 3+(-12)+9 | B. | 5+(-11)+7 | C. | (-7)+(-6)+12 | D. | (-5)+10+(-2) |
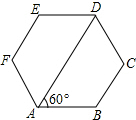 如图,六边形ABCDEF的内角都相等,∠DAB=60°.求证:AB∥ED,BC∥EF.
如图,六边形ABCDEF的内角都相等,∠DAB=60°.求证:AB∥ED,BC∥EF.