题目内容
19.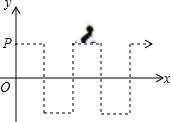 如图,在直角坐标系中,一只蚂蚁从点P(0,1)出发,沿着图示折线方向移动,第一次到达点(1,1),第二次达到点(1,0),第三次达到点(1,-1),第四次达到点(2,-1),…,按照这样的规律,第2016次到达点的坐标应为(672,1).
如图,在直角坐标系中,一只蚂蚁从点P(0,1)出发,沿着图示折线方向移动,第一次到达点(1,1),第二次达到点(1,0),第三次达到点(1,-1),第四次达到点(2,-1),…,按照这样的规律,第2016次到达点的坐标应为(672,1).
分析 设第n次到达的点为Pn,根据点的运动规律罗列出部分点P的坐标,根据点的变化找出变化规律“P6n(2n,1),P6n+1(2n+1,1),P6n+2(2n+1,0),P6n+3(2n+1,-1),P6n+4(2n+2,-1),P6n+5(2n+2,0)(n为自然数)”,根据此规律即可解决问题.
解答 解:设第n次到达的点为Pn,
观察,发现规律:P0(0,1),P1(1,1),P2(1,0),P3(1,-1),P4(2,-1),P5(2,0),P6(2,1),…,
∴P6n(2n,1),P6n+1(2n+1,1),P6n+2(2n+1,0),P6n+3(2n+1,-1),P6n+4(2n+2,-1),P6n+5(2n+2,0).(n为自然数)
∵2016=6×336,
∴P2016点的坐标为(2×336,1)=(672,1).
故答案为:(672,1).
点评 本题考查了规律型中的点的坐标,解题的关键是找出规律“P6n(2n,1),P6n+1(2n+1,1),P6n+2(2n+1,0),P6n+3(2n+1,-1),P6n+4(2n+2,-1),P6n+5(2n+2,0)(n为自然数)”.本题属于中档题,难度不大,解决该题型题目时,根据点P的变化罗列出部分点的坐标,再根据坐标的变化找出规律是关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
14.在下列多项式的乘法中,可用平方差公式计算的是( )
| A. | (-x+2)(x-2) | B. | (5a-3ab)(-5b-3ab) | C. | (a+b-c)(a-b-c) | D. | (x2+y)(x-y2) |
4.下列计算正确的是( )
| A. | a4÷a3=1 | B. | a4+a3=a7 | C. | (2a3)4=8a12 | D. | a4•a3=a7 |
9. 如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )
如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )
 如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )
如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )| A. | 55° | B. | 45° | C. | 30° | D. | 60° |
 在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=150°.
在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=150°.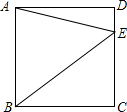 如图,点E在正方形ABCD的边CD上,若△ABE的面积为8,DE=1,则线段BE=5.
如图,点E在正方形ABCD的边CD上,若△ABE的面积为8,DE=1,则线段BE=5.