题目内容
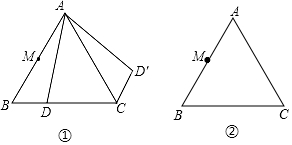
16.如图,△ABC是边长为2的等边三角形,M是AB的中点,点D在边BC上滑动,将△ABD顺时针旋转(少于360°).(1)如图①,若经过旋转后△ABD到达△ACD′的位置,则:①旋转中心是A,旋转角为60°;②画出点M旋转后的对应点M′,并指出:点M与点M′之间的距离为1.
(2)将△ABD绕点A作任意旋转,得△AB′D′(点D的对应点为D′),求线段MD′的最大值与最小值.(利用图②进行探究)
分析 (1)①根据中心旋转的定义即可解决问题;②利用三角形中位线定理即可解决问题;
(2)①当AD⊥BC时,△ABD旋转到如图位置时,MD′最小,最小值为$\sqrt{3}$-1.②当D与C重合时,△ABD旋转到如图位置时,MD′最大最大值,最大值为3.
解答 解:(1)①如图①中,旋转中心是A,旋转角为60°.
②点M′是AC的中点,MM′是△ABC的中位线,MM′=$\frac{1}{2}$BC=1.
故答案为A,60°,1.
(2)①当AD⊥BC时,△ABD旋转到如图位置时,MD′最小,最小值为$\sqrt{3}$-1.
②当D与C重合时,△ABD旋转到如图位置时,MD′最大最大值,最大值为3.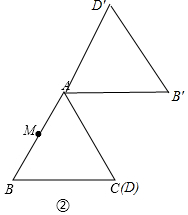
综上所述,MD′的最小值为$\sqrt{3}$-1,最大值为3.
点评 本题考查作图-旋转变换、等边三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
8.若∠α与∠β互余.∠α与∠γ互补,则下列中不可能成立的是( )
| A. | α=135°+$\frac{β+γ}{2}$ | B. | γ>β+45° | ||
| C. | ∠β与∠γ有可能互补 | D. | α+β+γ<270° |
 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.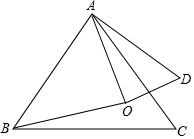 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,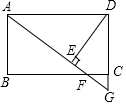 长方形ABCD中,点F为BC边上一点,AF延长线交DC延长线于点G,DE⊥AG于点E,DE=DC,求证:△ABF≌△DEA.
长方形ABCD中,点F为BC边上一点,AF延长线交DC延长线于点G,DE⊥AG于点E,DE=DC,求证:△ABF≌△DEA.