题目内容
6．
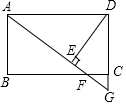长方形ABCD中，点F为BC边上一点，AF延长线交DC延长线于点G，DE⊥AG于点E，DE=DC，求证：△ABF≌△DEA．
分析 证出AB=DE，∠BFA=∠DAE，由AAS证明△ABF≌△DEA．
解答 证明：∵四边形ABCD是矩形，
∴AB=CD，AD∥BC，
又∵DE=DC，
∴AB=DE，
∵AD∥BC，
∴∠BFA=∠DAE，
∴在△ABF和△DEA中，$\left\{\begin{array}{l}{∠BFA=∠DAE}&{\;}\\{∠B=∠DEA=90°}&{\;}\\{AB=DE}&{\;}\end{array}\right.$，
∴△ABF≌△DEA．
点评 本题考查矩形的性质以及全等三角形的判定和性质，关键是知道矩形的四个角为直角，对边相等．
练习册系列答案
金钥匙试卷系列答案
相关题目
如图，CD⊥AB，点E、F在AB上，且CE=10cm，CD=8cm，CF=12cm，则点C到AB的距离是8cm．
如图，已知OA⊥OB，OC⊥OD，且∠AOD：∠BOC=4：5，求∠BOC的度数．
7．学校体育室有两个球筐，已知甲筐内的球比乙筐内球的个数的2倍还多4只． 现进行如下操作：第一次，从甲筐中取一只球放入乙筐；第二次，又从甲筐取出若干球放入乙筐，这次取出的球的个数是第一次移动后乙筐内球的个数的两倍．
若设乙球筐内原来有a只球
（1）请你填写下表（用含a的代数式表示）
（2）根据以上表格，化简后可知甲球筐内最后还剩下1个球．
（3）若最后乙球筐内有球27只，请求a的值．
若设乙球筐内原来有a只球
（1）请你填写下表（用含a的代数式表示）
| 甲球筐内球的个数 | 乙球筐内球的个数 | |
| 原来： | 2a+4 | a |
| 第一次后： | 2a+3 | a+1 |
| 第二次后： | 11 | 3a+3 |
（3）若最后乙球筐内有球27只，请求a的值．
