题目内容
9.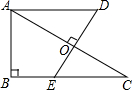 如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为$\frac{169}{24}$.
如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为$\frac{169}{24}$.
分析 连接AE,根据垂直平分线的性质可得AE=EC,然后在直角△ABE中利用勾股定理即可列方程求得EC的长,然后证明△AOD≌△COE,即可求得.
解答 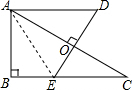 解:连接AE.
解:连接AE.
∵DE是线段AC的垂直平分线,
∴AE=EC.
设EC=x,则AE=EC=x,BE=BC-EC=12-x,
∵在直角△ABE中,AE2=AB2+BE2,
∴x2=52+(12-x)2,
解得:x=$\frac{169}{24}$.
即EC=$\frac{169}{24}$.
∵AD∥BC,
∴∠D=∠OEC,
在△AOD和△COE中,
$\left\{\begin{array}{l}{∠D=∠OEC}\\{∠AOD=∠COE}\\{OA=OC}\end{array}\right.$,
∴△AOD≌△COE,
∴AD=EC=$\frac{169}{24}$.
故答案是:$\frac{169}{24}$.
点评 本题考查了线段的垂直平分线的性质以及全等三角形的判定与性质,正确列方程求得EC的长是关键.

练习册系列答案
相关题目
18.纳米是一种长度单位,1纳米=10-9米.已知某种花粉的直径为35000纳米,则用科学记数法表示该花粉的直径为( )
| A. | 3.5×10-6m | B. | 3.5×10-5m | C. | 35×10-4m | D. | 3.5×104m |
19.2015年9月20日,吉图珺高铁正式开通运营,使长春至军春通勤时间缩短至3小时左右,项目总投资416亿元,416亿这个数用科学记数法表示为( )
| A. | 416×108 | B. | 41.6×109 | C. | 4.16×1010 | D. | 4.16×1011 |
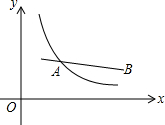 如图,已知线段AB,点A的坐标为(1,$\frac{3}{2}$),点B的坐标为(4,1),反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB有交点,则k的取值范围为$\frac{3}{2}$≤k≤4.
如图,已知线段AB,点A的坐标为(1,$\frac{3}{2}$),点B的坐标为(4,1),反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB有交点,则k的取值范围为$\frac{3}{2}$≤k≤4.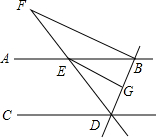 如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=50°,∠F=25°.
如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=50°,∠F=25°.