Question

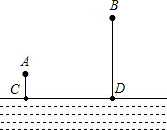如图，A、B两个化工厂在河道CD的同侧，A、B两厂到河的距离分别为AC=2km，BD=3km，CD=12km，现在河边CD上建污水处理站，将A、B两厂输送的污水处理后再排入河道，设铺设排污水管的费用为20000元/千米，请你在河道CD边上选择污水站位置O，使铺设排污水管的费用最省，并求出铺设排污水管的总费用？

Answer 1

考点：轴对称-最短路线问题,作图—应用与设计作图

专题：

分析：作点A关于河CD的对称点A'，连接A'B交河CD于O点，根据轴对称确定最短路线问题，点O就是水厂的位置；构造出以A′B为斜边的直角三角形，利用勾股定理列式计算即可求出A′B，再乘以单价计算即可得解．

解答：解：如图所示；
作点A关于河CD的对称点A'，连接A'B交河CD于O点，则点O就是水厂的位置，此时水管道最短，最短长度=AO+BO=A′O+BO=A′B；
作出以A′B为斜边的直角三角形，
∵AC=2km，BD=3km，CD=12km，
∴A′E=CD=12km，BE=2+3=5km，
由勾股定理得，A′B=

A′E2+BE2

=

122+52

=13km，
20 000×13=260 000元．
答：铺设水管的总费用260000元．

点评：本题考查了轴对称确定最短路线问题，勾股定理，熟练掌握最短路线的确定方法是解题的关键．