题目内容
3．
如图，AB∥CD，∠B=70°，∠E=20°，求∠D的度数．
分析 根据平行线的性质得∠BFD=∠B=70°，再根据三角形的一个外角等于与它不相邻的两个内角和，得∠D=∠BFD-∠E，由此即可求∠D．
解答 解：∵AB∥CD，∠B=70°，
∴∠BFD=∠B=70°，
∵∠BFD是△DEF的外角，
∴∠D=∠BFD-∠E=70°-20°=50°．
点评 此题主要运用了平行线的性质以及三角形的一个外角等于和它不相邻的两个内角和．
练习册系列答案
小学期末标准试卷系列答案
相关题目
13．下列各式计算正确的是（ ）
| A． | 2$\sqrt{3}$-$\sqrt{3}$=2 | B． | 2$\sqrt{3}$+$\sqrt{2}$=2$\sqrt{5}$ | C． | 4$\sqrt{2}$×2$\sqrt{2}$=8$\sqrt{2}$ | D． | 4$\sqrt{6}$÷2$\sqrt{2}$=2$\sqrt{3}$ |
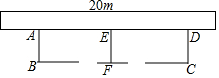如图，星光中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙（墙的长度为20m），其余部分用篱笆围成，且中间用一段篱笆把它分隔成了两个矩形，两个矩形各留一道1m宽的门，已知篱笆的总长度为34m．
在全国初中数学联赛中，将参赛两个班学生的成绩（得分均为整数）进行整理后分成五组，绘制出如下的频率分布直方图（如图所示），已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10，第二组的频数是40．
13．
如图，四边形ABCD为⊙O的内接四边形，已知∠AOC=100°，则∠ADC的度数为（ ）
如图，四边形ABCD为⊙O的内接四边形，已知∠AOC=100°，则∠ADC的度数为（ ）| A． | 50° | B． | 80° | C． | 100° | D． | 130° |