题目内容
13．
如图，四边形ABCD为⊙O的内接四边形，已知∠AOC=100°，则∠ADC的度数为（ ）| A． | 50° | B． | 80° | C． | 100° | D． | 130° |
分析 先依据圆周角定理求得∠B的度数，然后再依据内接四边形的性质求得∠ADC的度数即可．
解答 解：∵∠AOC=100°，
∴∠B=$\frac{1}{2}∠$AOC=50°，
∴∠ADC=180°-∠B=130°，
故选D．
点评 本题主要考查的是圆内接四边形的性质、圆周角定理的应用，求得∠B的度数是解题的关键．
练习册系列答案
相关题目
如图，AB∥CD，∠B=70°，∠E=20°，求∠D的度数．
4．
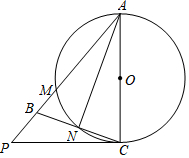如图，在△ABC中，AB=AC，以AC为直径的⊙O交与点M，交BC于点N，连接AN，过点C的切线交AB的延长线于点P．
（1）求证：∠BCD=∠BAN．
（2）若AC=4，PC=3，求MN•BC的值．
如图，在△ABC中，AB=AC，以AC为直径的⊙O交与点M，交BC于点N，连接AN，过点C的切线交AB的延长线于点P．（1）求证：∠BCD=∠BAN．
（2）若AC=4，PC=3，求MN•BC的值．
8．
如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD=2CD，点E，F分别为AB，AD的中点，则三角形AEF与多边形BCDFE的面积之比为（ ）
如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD=2CD，点E，F分别为AB，AD的中点，则三角形AEF与多边形BCDFE的面积之比为（ ）| A． | 1：7 | B． | 1：6 | C． | 1：5 | D． | 1：4 |
18．已知函数y=（k-3）x2+2x+1的图象与x轴有交点，则k的取值范围是（ ）
| A． | k＜4且k≠3 | B． | k≤4且k≠3 | C． | k＜4 | D． | k≤4 |