题目内容
15.已知函数y=-$\frac{1}{2}$(x+1)2-1.(1)指出函数图象的开口方向、对称轴和顶点分别为开口方向向下、对称轴为x=-1、顶点坐标为(-1,-1);
(2)当x≥-1 (或>-1)时,y随x的增大而减小;
(3)怎样移动抛物线y=-$\frac{1}{2}$x2就可以得到抛物线y=-$\frac{1}{2}$(x+1)2-1.
分析 (1)利用二次根式的性质确定出开口方向,顶点坐标以及对称轴即可;
(2)由对称轴和开口方向得出增减性;
(3)根据平移规律回答问题.
解答 解:(1)∵a=-$\frac{1}{2}$<0,
∴抛物线开口向下,
顶点坐标为(-1,-1),对称轴为直线x=1;
故答案是:开口方向向下、对称轴为x=-1、顶点坐标为(-1,-1);
(2)∵对称轴x=-1,
∴当x>-1时,y随x的增大而减小.
故答案是:≥-1 (或>-1);
(3)向左平移1个单位长度,再向下平移1个单位长度移动抛物线y=-$\frac{1}{2}$x2就可以得到抛物线y=-$\frac{1}{2}$(x+1)2-1.
点评 本题考查了二次函数的性质,由二次函数的性质求抛物线的对称轴和顶点坐标,最值,增减性是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB∥CD,∠B=70°,∠E=20°,求∠D的度数.
如图,AB∥CD,∠B=70°,∠E=20°,求∠D的度数.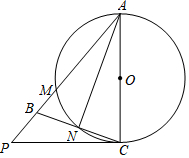 如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.