题目内容
在△ABC中,不能判断△ABC为直角三角形的条件是( )
| A、∠C=∠A-∠B | ||||
| B、∠A:∠B:∠C=5:2:3 | ||||
C、a=
| ||||
| D、a:b:c=2:2:4 |
考点:勾股定理的逆定理,三角形内角和定理
专题:
分析:根据三角形的内角和定理和勾股定理的逆定理,分别对每一项进行判断即可.
解答:解:A、∵∠C=∠A-∠B,∴∠A=∠B+∠C,∴∠A=90°,故能判定△ABC是直角三角形;
B、∵∠A:∠B:∠C=5:2:3,∴∠A=∠B+∠C,∴∠A=90°,故能判定△ABC是直角三角形;
C、∵a=
c,b=
c,∴a2+b2=
c2+
c2=c2,故能判定△ABC是直角三角形;
D、∵a:b:c=2:2:4,∴a2+b2≠c2,故不能判定△ABC是直角三角形;
故选D.
B、∵∠A:∠B:∠C=5:2:3,∴∠A=∠B+∠C,∴∠A=90°,故能判定△ABC是直角三角形;
C、∵a=
| 3 |
| 5 |
| 4 |
| 5 |
| 9 |
| 25 |
| 16 |
| 25 |
D、∵a:b:c=2:2:4,∴a2+b2≠c2,故不能判定△ABC是直角三角形;
故选D.
点评:本题考查了勾股定理的逆定理的应用,判断三角形是否为直角三角形,可利用勾股定理的逆定理和直角三角形的定义判断,此题比较容易.

练习册系列答案
相关题目
数轴上点A表示-1.5,若将点A沿着数轴的正方向移动3个单位,然后向负方向移动2.5个单位,则点B最终所表示的实数为( )
| A、-1 | B、-1.5 | C、4 | D、7 |
在直角坐标系中,点A(a,5),B(3,b)关于x轴对称,则a+b=( )
| A、-8 | B、2 | C、-2 | D、8 |
下列命题中,正确的是( )
| A、相似三角形是全等的三角形 |
| B、一个角为30°的两个等腰三角形相似 |
| C、全等三角形都是相似三角形 |
| D、所有等腰直角三角形不一定相似 |
若A=4x2-3x-2,B=4x2-3x-4,则A,B的大小关系是( )
| A、A<B | B、A=B |
| C、A>B | D、无法确定 |
代数式a2、-xyz、
、-x、
、0、a2+b2、-0.2中单项式的个数是( )
| ab2 |
| 4 |
| b |
| a |
| A、4 | B、5 | C、6 | D、7 |
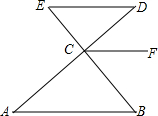 如图,已知∠B=∠E,∠A=∠FCD,试问ED与CF平行吗?为什么?
如图,已知∠B=∠E,∠A=∠FCD,试问ED与CF平行吗?为什么?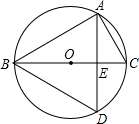 如图所示,BC为⊙O的直径,弦AD⊥BC于E,∠C=60°.
如图所示,BC为⊙O的直径,弦AD⊥BC于E,∠C=60°.