题目内容

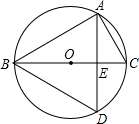如图所示，BC为⊙O的直径，弦AD⊥BC于E，∠C=60°．
求证：△ABD为等边三角形．
考点：圆周角定理,等边三角形的判定
专题：证明题
分析：根据垂径定理求出AE=DE，根据线段垂直平分线性质得出BA=BD，根据圆周角定理求出∠D=60°，根据等边三角形判定推出即可．
解答：证明：∵BC为⊙O的直径，AD⊥BC，
∴AE=DE，
∴BD=BA，
∵∠D=∠C=60°，
∴△ABD为等边三角形．
点评：本题考查了垂径定理，线段垂直平分线性质，圆周角定理，等边三角形判定的应用，主要考查学生的推理能力．
练习册系列答案
相关题目
在△ABC中，不能判断△ABC为直角三角形的条件是（　　）
A、∠C=∠A-∠B
B、∠A：∠B：∠C=5：2：3
C、a=
3
5
c，b=
4
5
c
D、a：b：c=2：2：4
解方程：
（1）y2-5y+2=0
（2）（x-1）（x+2）=10．
如图，已知数轴上有A、B、C三个点，它们表示的数分别是-24，-10，10．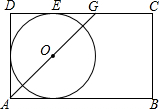
（1）填空：AB=
 
，BC=
 
；
（2）若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动．设运动时间为t，用含t的代数式表示BC和AB的长，试探索：BC-AB的值是否随着时间t的变化而改变？请说明理由．
（3）现有动点P、Q都从A点出发，点P以每秒1个单位长度的速度向终点C移动；当点P移动到B点时，点Q才从A点出发，并以每秒3个单位长度的速度向右移动，且当点P到达C点时，点Q就停止移动．设点P移动的时间为t秒，问：当t为多少时P、Q两点相距6个单位长度？
如图，矩形ABCD，∠DAB的平分线交DC于点G，O是AG的中点，⊙O与DG相切，切点为E，
（1）求证：E点是DG的中点；
（2）求证：AD是⊙O的切线．
某饮料经营部每天的固定成本为200元，其销售的饮料每瓶进价为5元．销售单价与日平均销售的关系如表：
销售单价（元） 6 6.5 7 7.5 8 8.5 9
日平均销售量（瓶） 480 460 440 420 400 380 360
（1）若记销售单价比每瓶进价多x元，则销售单价为
 
元，日销售量为
 
元 （用含x的代数式表示）；求日均毛利润（毛利润=总售价-总进价-固定成本）y与x之间的函数关系式．
（2）若要使日均毛利润达到1400元，则销售单价应定为多少元？
（3）若要使日均毛利润达到最大，销售单价应定为多少元？最大日均毛利润为多少元？
已知：在△ABC中，AC=BC，∠ACB=90°，过点C作CD⊥AB于点D，点E是AB边上一动点（不含端点A、B），连接CE，过点B作CE的垂线交直线CE于点F，交直线CD于点G（如图①）．
（1）求证：AE=CG；
（2）若点E运动到线段BD上时（如图②），试猜想AE、CG的数量关系是否发生变化，请直接写出你的结论；
（3）过点A作AH垂直于直线CE，垂足为点H，并交CD的延长线于点M（如图③），找出图中与BE相等的线段，并证明．
36×(
2
3
-
3
4
-
1
12
)-(-2)3．
如图，公园要在一个圆形的喷水池中央垂直于水面处安装一个柱子OA，O恰在水面中心，OA=1.25m，由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计成水流在离OA的距离为1m处达到距水面的距离最大，高度为2.25m．若不计其它因素，那么水池的半径至少要多少米才能使喷出的水流不致落到池外？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网