题目内容
13.已知关于x的不等式ax+2<πx+b,a可以取任意实数,b为大于2的任意实数.(1)解此不等式;
(2)如果此不等式对一切x<0恒成立,试确定a的取值范围.
分析 (1)先移项,再合并得(a-π)x<b-2,然后讨论:当a>π或a=π或a<π时,分别解不等式即可;
(2)利用b>2,即b-2>0,当a≥π,对于(a-π)x<b-2,对一切x<0恒成立.
解答 解:(1)移项得ax-πx<b-2,
合并得(a-π)x<b-2,
当a>π时,x<$\frac{b-2}{a-π}$;
当a=π时,x为任意实数;
当a<π时,x>$\frac{b-2}{a-π}$;
(2)当x<0时,
而b>2,
所以a-π≥0,即a≥π.
点评 本考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.解决本题的关键是讨论a的范围.

练习册系列答案
相关题目
4.已知直线y=-x+4与x轴、y轴分别交于A,B两点,与反比例函数y=$\frac{k}{x}$(k>0)的图象交于C,D两点,若AB=$\sqrt{2}$CD,则k的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
8.函数$y=(a-2){x^{{a^2}-2}}$是反比例函数,则a的值是( )
| A. | 1或-1 | B. | -2 | C. | 2 | D. | 2或-2 |
18.已知点D与点A(-2,0),B(0,4),C(a,a)是一平行四边形的四个顶点,则CD长的最小值为( )
| A. | 4 | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
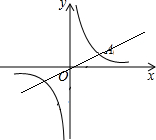 已知一次函数y=kx与反比例函数y=$\frac{3}{x}$的图象都经过点A(m,1).求:
已知一次函数y=kx与反比例函数y=$\frac{3}{x}$的图象都经过点A(m,1).求: 如图,分别以△ABC的三边为边,在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR,连接PA,AQ,QR,RP,那么四边形PRQA是平行四边形吗?证明你的结论.
如图,分别以△ABC的三边为边,在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR,连接PA,AQ,QR,RP,那么四边形PRQA是平行四边形吗?证明你的结论.