题目内容
8.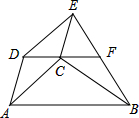 如图,四边形ABCD中,AB∥DC,以AC,AD为边作?ACED,DG的延长线交BE于F,求证:EF=FB.(请用多种证明方法)
如图,四边形ABCD中,AB∥DC,以AC,AD为边作?ACED,DG的延长线交BE于F,求证:EF=FB.(请用多种证明方法)
分析 已知条件为DC∥AB,可再作一条平行线来构造平行四边形,得到F为新平行四边形的对角线的交点.
解答 证明:方法一:过点B作BG∥AD,交DC的延长线于G,连接EG,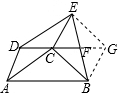
∵DC∥AB,
∴四边形ABGD是平行四边形,
∴BG平行且等于AD.
在四边形ACED中,AD∥CE且AD=CE,
∴CE∥BG且CE=BG.
∴四边形BCEG为平行四边形.
∴EF=FB;
方法二:延长EC交AB于G,如图,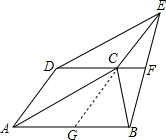
∵EC∥AD,DC∥AB,
∴CG=AD,
又∵AD=CE,
∴EC=GC,
∵DF∥AB,
∴EF=FB
点评 本题考查了平行四边形的判定与性质,三角形的问题通常也转换为平行四边形的问题来解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.[x]表示不超过实数x的最大整数(如[π]=3,[-π]=-4,[-4]=-4,记M=[x]+[2x]+[3x]将不能表示成M形式的正整数称为“隐形数”.则不超过2014的“隐形数”的个数是( )
| A. | 335 | B. | 336 | C. | 670 | D. | 671 |
18.已知点D与点A(-2,0),B(0,4),C(a,a)是一平行四边形的四个顶点,则CD长的最小值为( )
| A. | 4 | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
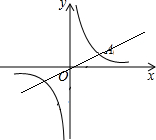 已知一次函数y=kx与反比例函数y=$\frac{3}{x}$的图象都经过点A(m,1).求:
已知一次函数y=kx与反比例函数y=$\frac{3}{x}$的图象都经过点A(m,1).求: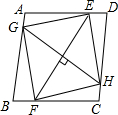 如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形. 如图,AB=DC.
如图,AB=DC.