题目内容
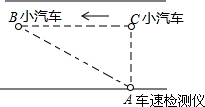规定：小汽车在城市街路上行驶速度不得超过60千米/小时，一辆小汽车在一条城市道路上自右向左行驶，某一时刻刚好行驶道路对面车速检测仪A的正前方C处，AC=30米．过了2秒后到达B处，测得小汽车与车速检测仪之间的距离AB为50米．这辆小汽车超速了吗？为什么？超速了多少？考点：勾股定理的应用
专题：
分析：首先利用勾股定理求得BC的长，然后利用速度、时间及路程之间的关系求得小车的速度，比较后即可得到答案．
解答：解：在Rt△ABC中，AC=30m，AB=50m；
据勾股定理可得：BC=
=40（m）
∴小汽车的速度为v=40÷2=20（m/s）=20×3.6（km/h）=72（km/h）；
∵72（km/h）＞60（km/h）；
∴这辆小汽车超速行驶．
超速：72-60=12（km/h）．
据勾股定理可得：BC=
| 502-402 |
∴小汽车的速度为v=40÷2=20（m/s）=20×3.6（km/h）=72（km/h）；
∵72（km/h）＞60（km/h）；
∴这辆小汽车超速行驶．
超速：72-60=12（km/h）．
点评：考查了勾股定理的知识，解题的关键是从实际问题中抽象出直角三角形，难度不大．
练习册系列答案
相关题目
几个棱长为2的正方体组成的几何体从正面、左面以及上面看得出的平方平面图形如图所示，则这个几何体的体积是（ ）
| A、32 | B、40 | C、48 | D、56 |
直线y=kx+b经过A（-1，1）和B（-
如图，在Rt△ABC中，∠C=90°，AB=2BC，则sinB的值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
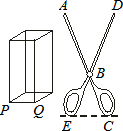有一支夹子如图所示，AB=2BC，BD=2BE，在夹子前面有一个长方体硬物，厚PQ为6cm，如果想用夹子的尖端A、D两点夹住P、Q两点，那么手握的地方EC至少要张开