题目内容
已知直线y=kx+b与直线y=3x平行且经过点(-3,y1)、B(-7,y2),则y1 y2(填“<”或“>”或“=”).
考点:一次函数图象上点的坐标特征
专题:
分析:先根据直线y=kx+b与直线y=3x平行得出k=3,再根据一次函数的性质判断出函数的增减性,根据-3>-7即可得出结论.
解答:解:∵直线y=kx+b与直线y=3x平行,
∴k=3,
∴函数y=kx+b是增函数.
∵点(-3,y1)、B(-7,y2)在此直线上,且-3>-7,
∴y1>y2.
故答案为:>.
∴k=3,
∴函数y=kx+b是增函数.
∵点(-3,y1)、B(-7,y2)在此直线上,且-3>-7,
∴y1>y2.
故答案为:>.
点评:本题考查的是一次函数图形上点的坐标点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,商场采取降价措施,假设一定范围内,衬衫单价每降1元,商场平均每天可多售出2件.如果销售这批衬衫每天盈利1250元,设衬衫单价降了x元,根据题意,可列方程( )
| A、(40-x)(20+2x)=1250 |
| B、(40-2x)(20+x)=1250 |
| C、(40+x)(20-2x)=1250 |
| D、(40+2x)(20-x)=1250 |
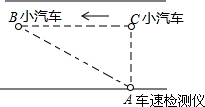 规定:小汽车在城市街路上行驶速度不得超过60千米/小时,一辆小汽车在一条城市道路上自右向左行驶,某一时刻刚好行驶道路对面车速检测仪A的正前方C处,AC=30米.过了2秒后到达B处,测得小汽车与车速检测仪之间的距离AB为50米.这辆小汽车超速了吗?为什么?超速了多少?
规定:小汽车在城市街路上行驶速度不得超过60千米/小时,一辆小汽车在一条城市道路上自右向左行驶,某一时刻刚好行驶道路对面车速检测仪A的正前方C处,AC=30米.过了2秒后到达B处,测得小汽车与车速检测仪之间的距离AB为50米.这辆小汽车超速了吗?为什么?超速了多少?