题目内容
3.某市为处理污水需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时每天比原计划多铺设10米,结果提前20天完成任务,设原计划每天铺设管道x米,则可得方程( )| A. | $\frac{4000}{x}=\frac{4000}{x+10}+20$ | B. | $\frac{4000}{x}=\frac{4000}{x-10}-2}$ | ||
| C. | $\frac{4000}{x+10}=\frac{4000}{x}+20$ | D. | $\frac{4000}{x-10}=\frac{4000}{x}-20$ |
分析 所求的是原计划的工效,工作总量是4000,一定是根据工作时间来列的等量关系.本题的关键描述语是:“结果提前20天完成任务”;等量关系为:原计划用的时间=实际用的时间+20.
解答 解:设原计划每天铺设管道x米,则原计划用的时间为:$\frac{4000}{x}$,实际用的时间为:$\frac{4000}{x+10}$.
所列方程为:$\frac{4000}{x}$=$\frac{4000}{x+10}$+20.
故选A.
点评 本题考查了由实际问题抽象出分式方程,应用题中一般有三个量,求一个量,明显的有一个量,一定是根据另一量来列等量关系的.本题应用的等量关系为:工作时间=工作总量÷工效.

练习册系列答案
相关题目
13.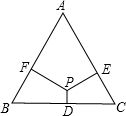 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{20}{3}$ | C. | 7 | D. | 8 |
14. 如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )
如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )
 如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )
如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )| A. | 6cm | B. | 7cm | C. | 10cm | D. | 12cm |
11. 如图,直线a∥b,若∠1=45°,∠2=55°,则∠3等于( )
如图,直线a∥b,若∠1=45°,∠2=55°,则∠3等于( )
 如图,直线a∥b,若∠1=45°,∠2=55°,则∠3等于( )
如图,直线a∥b,若∠1=45°,∠2=55°,则∠3等于( )| A. | 80° | B. | 90° | C. | 955° | D. | 100° |
 在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有3个.
在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有3个.