题目内容
14. 如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )
如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )| A. | 6cm | B. | 7cm | C. | 10cm | D. | 12cm |
分析 根据折叠的性质可得EF=AE、BF=BA,从而?ABCD的周长可转化为:△FDE的周长+△FCB的周长,求出AB+BC,再由△FCB的周长为42,求出FC的长,即可解决问题.
解答 解:由折叠的性质可得EF=AE、BF=AB,
∴?ABCD的周长=DF+FC+CB+BA+AE+DE=△FDE的周长+△FCB的周长=10+24=34,
∵四边形ABCD为平行四边形,
∴AB+BC=17,
∵△FCB的周长=CF+BC+BF=CF+BC+AB=24,
即FC+17=24,
∴FC=7cm,
故选B.
点评 本题主要考查了翻折变换的性质、平行四边形的性质等几何知识点;根据折叠的性质将平行四边形的周长与△FCB的周长进行转化是解决问题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
9.2017年3月份工业和信息化部公布的数据显示,2016年我国全年共生产手机21亿部,将数据21亿用科学记数法表示为( )
| A. | 2.1×108 | B. | 21×108 | C. | 2.1×109 | D. | 0.21×1010 |
19.2016年我国就业形势总体稳定,超过全年预期目标,成为经济运行的一大亮点,城镇新增就业1312万人,这个数据用科学记数法可以表示为( )
| A. | 1.312×106人 | B. | 1.312×107人 | C. | 13.12×106人 | D. | 0.1312×108人 |
3.某市为处理污水需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时每天比原计划多铺设10米,结果提前20天完成任务,设原计划每天铺设管道x米,则可得方程( )
| A. | $\frac{4000}{x}=\frac{4000}{x+10}+20$ | B. | $\frac{4000}{x}=\frac{4000}{x-10}-2}$ | ||
| C. | $\frac{4000}{x+10}=\frac{4000}{x}+20$ | D. | $\frac{4000}{x-10}=\frac{4000}{x}-20$ |
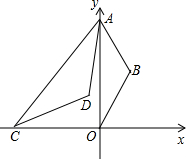 如图,点A为y轴正半轴上一点,以OA为底边向y轴右侧作等腰三角形OAB,使得∠B=120°,C为x轴上一点,连接AC,以AC为底边向右侧作等腰三角形ACD,使得∠D=120°.
如图,点A为y轴正半轴上一点,以OA为底边向y轴右侧作等腰三角形OAB,使得∠B=120°,C为x轴上一点,连接AC,以AC为底边向右侧作等腰三角形ACD,使得∠D=120°.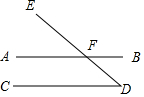 如图,∠D=49°,∠BFE=131°,试用三种不同的方法说明AB∥CD.
如图,∠D=49°,∠BFE=131°,试用三种不同的方法说明AB∥CD.