题目内容
7.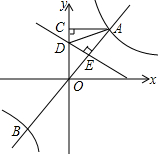 如图,过原点O的直线AB与反比例函数y=$\frac{k}{x}$(k>0)的图象交于A、B两点,点B坐标为(-2,m),过点A作AC⊥y轴于点C,OA的垂直平分线DE交OC于点D,交AB于点E.若△ACD的周长为5,则k的值为6.
如图,过原点O的直线AB与反比例函数y=$\frac{k}{x}$(k>0)的图象交于A、B两点,点B坐标为(-2,m),过点A作AC⊥y轴于点C,OA的垂直平分线DE交OC于点D,交AB于点E.若△ACD的周长为5,则k的值为6.
分析 根据题意得到A、B两点关于原点对称,得到点A坐标为(2,-m),求得AC=2,由于DE垂直平分AO,得到AD=OD,根据△ACD的周长为5,求出OC=AD+CD=3,得到A(2,3),即可得到结果.
解答 解: ∵过原点O的直线AB与反比例函数y=$\frac{k}{x}$(k>0)的图象交于A、B两点,
∵过原点O的直线AB与反比例函数y=$\frac{k}{x}$(k>0)的图象交于A、B两点,
∴A、B两点关于原点对称,
∵点B坐标为(-2,m),
∴点A坐标为(2,-m),
∵AC⊥y轴于点C,
∴AC=2,
∵DE垂直平分AO,
∴AD=OD,
∵△ACD的周长为5,
∴AD+CD=5-AC=3,
∴OC=AD+CD=3,
∴A(2,3),
∵点A在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴k=2×3=6,
故答案为:6.
点评 本题考查了一次函数与反比例函数的交点问题,线段的垂直平分线的性质,三角形的周长,得出OC=AD+CD是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列运算正确的是( )
| A. | 3a2•a3=3a6 | B. | 5x4-x2=4x2 | C. | (2a2)3•(-ab)=-8a7b | D. | 2x2÷2x2=0 |
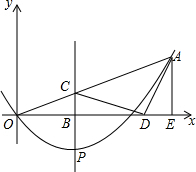 如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.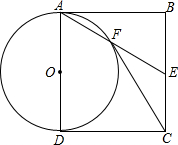 如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.