题目内容
10.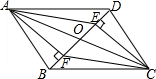 如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O,求证:AO=CO.
如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O,求证:AO=CO.
分析 由已知条件证得直角三角形全等,得出一组对边相等,再由∠AEB=∠CFD=90°,得到这组对边平行,得到四边形AECF是平行四边形,根据平行四边形的对角线互相平分得出结果.
解答 证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∵AB=CD,BE=DF,
在Rt△ABE与Rt△CDF中,$\left\{\begin{array}{l}{AB=CD}\\{BE=DF}\end{array}\right.$,
∴Rt△ABE≌Rt△CDF(HL),
∴AE=CF,
又∵∠AEB=∠CFD=90°,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AO=CO(平行四边形的对角线互相平分).
点评 此题主要考查了全等三角形的判定与性质,平行四边形的判定与性质,得出一组对边平行且相等是解题关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
1. 如图,AB∥DC,∠1=110°,则∠A的度数为( )
如图,AB∥DC,∠1=110°,则∠A的度数为( )
 如图,AB∥DC,∠1=110°,则∠A的度数为( )
如图,AB∥DC,∠1=110°,则∠A的度数为( )| A. | 110° | B. | 80° | C. | 70° | D. | 60° |
18.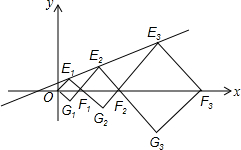 在平面直角坐标系中,点E1,E2,E3,…,和F1,F2,F3,…分别在直线y=kx+b和x轴上,四边形OE1F1G1,四边形F1E2F2G2,四边形F2E3F3G3,…都是正方形,如果E1(1,1),E2(4,2),那么线段Fn-1Fn的长是( )
在平面直角坐标系中,点E1,E2,E3,…,和F1,F2,F3,…分别在直线y=kx+b和x轴上,四边形OE1F1G1,四边形F1E2F2G2,四边形F2E3F3G3,…都是正方形,如果E1(1,1),E2(4,2),那么线段Fn-1Fn的长是( )
 在平面直角坐标系中,点E1,E2,E3,…,和F1,F2,F3,…分别在直线y=kx+b和x轴上,四边形OE1F1G1,四边形F1E2F2G2,四边形F2E3F3G3,…都是正方形,如果E1(1,1),E2(4,2),那么线段Fn-1Fn的长是( )
在平面直角坐标系中,点E1,E2,E3,…,和F1,F2,F3,…分别在直线y=kx+b和x轴上,四边形OE1F1G1,四边形F1E2F2G2,四边形F2E3F3G3,…都是正方形,如果E1(1,1),E2(4,2),那么线段Fn-1Fn的长是( )| A. | 2n-1 | B. | 2n | C. | 22n | D. | 2n+1 |
15.在实数:3.141 59,$\root{3}{64}$,1.010 010 001…,4,2.$\stackrel{••}{01}$,2π,$\frac{22}{7}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.下面的图形是天气预报使用的图标,其中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则BC的长是( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |