题目内容
11.四边形的外角和是360°.分析 根据多边形的内角和定理和邻补角的关系即可求出四边形的外角和.
解答 解:∵四边形的内角和为(4-2)•180°=360°,
而每一组内角和相邻的外角是一组邻补角,
∴四边形的外角和等于4×180°-360°=360°,
故答案为:360.
点评 本题主要考查了多边形的内角和定理和多边形的外角和,比较简单.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
1. 如图,AB∥DC,∠1=110°,则∠A的度数为( )
如图,AB∥DC,∠1=110°,则∠A的度数为( )
 如图,AB∥DC,∠1=110°,则∠A的度数为( )
如图,AB∥DC,∠1=110°,则∠A的度数为( )| A. | 110° | B. | 80° | C. | 70° | D. | 60° |
2.下面的图形是天气预报使用的图标,其中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则BC的长是( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
1. 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )| A. | 70° | B. | 68° | C. | 60° | D. | 72° |
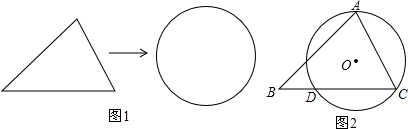
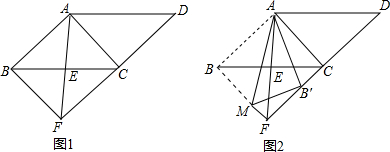
 如图,已知∠1=∠2,∠3=80°,则∠4=80°.
如图,已知∠1=∠2,∠3=80°,则∠4=80°.