题目内容
16. 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为($\sqrt{2}$,-$\sqrt{2}$).
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为($\sqrt{2}$,-$\sqrt{2}$).
分析 求出旋转后OA与y轴夹角为45°,然后求出点A′的横坐标与纵坐标,从而得解.
解答 解:∵三角板绕原点O顺时针旋转75°,
∴旋转后OA与y轴夹角为45°,
∵OA=2,
∴OA′=2,
∴点A′的横坐标为2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
纵坐标为-2×$\frac{\sqrt{2}}{2}$=-$\sqrt{2}$,
所以,点A′的坐标为($\sqrt{2}$,-$\sqrt{2}$).
故答案为:($\sqrt{2}$,-$\sqrt{2}$).
点评 本题考查了坐标与图形变化-旋转,准确识图求出旋转后OA与y轴的夹角为45°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.在Rt△ABC中,各边都扩大3倍,则角A的正弦值( )
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 不变 | D. | 不能确定 |


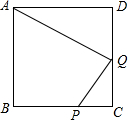 如图,已知正方形ABCD的边长AD=4,PC=1,CQ=DQ=2.求证:△ADQ∽△QCP.
如图,已知正方形ABCD的边长AD=4,PC=1,CQ=DQ=2.求证:△ADQ∽△QCP. 如图,顺次连接任意四边形ABCD各边中点,所得的四边形EFGH是中点四边形.下列四个叙述:
如图,顺次连接任意四边形ABCD各边中点,所得的四边形EFGH是中点四边形.下列四个叙述: