题目内容
6.某快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本).若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价x(元)取整数,用y(元)表示该店日净收入.(日净收入=每天的销售额-套餐成本-每天固定支出)(1)当5<x≤10时,y=400(x-5)-600;当x>10时,y=-40x2+100x-4600(x>10);
(2)若该店日净收入为1560元,为了优惠顾客,那么每份售价是多少元?
分析 (1)本题考查的是分段函数的知识点.当5<x≤10时,y=400(x-5)-600;
当x>10时,y=(x-5)[400-40(x-10)]-600;
(2)把y=1560代入(1)中的函数关系式.
解答 解:(1)由题意得:当5<x≤10时,y=400(x-5)-600;
当x>10时,y=(x-5)[400-40(x-10)]-600=-40x2+100x-4600.
即y=-40x2+100x-4600(x>10).
故答案是:400(x-5)-600;-40x2+100x-4600(x>10);
(2)由(1)知,y=-40x2+100x-4600(x>10)
当y=1560时,
(x-5)[400-40(x-10)]-600=1560,
解得:x1=11,x2=14,
经检验它们都是原方程的根,但为了优惠顾客,应该取x=11.
答:该店日净收入为1560元,那么每份售价是11元.
点评 本题考查的是二次函数的实际应用和一元二次方程的应用的有关知识,解题的关键是根据题目中的等量关系列出函数关系.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
14.下列计算正确的是( )
| A. | a5-a3=a2 | B. | (-a5)2=a10 | C. | a5•a3=a15 | D. | $\frac{{a}^{6}}{{a}^{3}}$=a2 |
1.下列说法正确的是( )
| A. | 若|a|=-a,则a<0 | B. | 式子3xy2-4x3y+12是七次三项式 | ||
| C. | 若a<0,ab<0,则b>0 | D. | 若a=b,m是有理数,则$\frac{a}{m}$=$\frac{b}{m}$ |
15.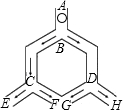 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为($\sqrt{2}$,-$\sqrt{2}$).
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为($\sqrt{2}$,-$\sqrt{2}$).