题目内容
6．已知关于x的一元二次方程x2-2x-k=0的一个根为3，则它的另一个根为（ ）| A． | -5 | B． | -1 | C． | 1 | D． | 5 |
分析 根据根与系数的关系，由两根之和可以求出方程的另一个根．
解答 解：设方程的另一个根是x1，则：
3+x1=2，
解得x1=-1．
即另一个根是-1．
故选B．
点评 本题考查的是一元二次方程的根与系数的关系；把方程的解代入方程求出字母系数k的值是解决问题的关键．
练习册系列答案
相关题目
12．
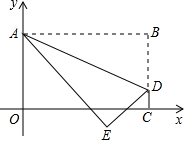如图，将矩形OABC置于平面直角坐标系中，点A的坐标为（0，4），点C在x轴上，点D（3$\sqrt{5}$，1）在BC上，将矩形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E．若抛物线y=ax2-4$\sqrt{5}$ax+10（a≠0且a为常数）的顶点落在△ADE的内部，则a的取值范围是（ ）
如图，将矩形OABC置于平面直角坐标系中，点A的坐标为（0，4），点C在x轴上，点D（3$\sqrt{5}$，1）在BC上，将矩形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E．若抛物线y=ax2-4$\sqrt{5}$ax+10（a≠0且a为常数）的顶点落在△ADE的内部，则a的取值范围是（ ）| A． | $\frac{2}{5}＜a＜\frac{13}{20}$ | B． | $\frac{2}{5}＜a＜\frac{11}{20}$ | C． | $\frac{11}{20}＜a＜\frac{3}{5}$ | D． | $\frac{3}{5}＜a＜\frac{13}{20}$ |
17．
如图，⊙O的半径为5，弦心距OC=3，则弦AB的长是（ ）
如图，⊙O的半径为5，弦心距OC=3，则弦AB的长是（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 5 |
已知，两数在数轴上的位置如图所示，则化简代数式|a+b|-|a-1|+|b+2|．
16．下列标志既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |