题目内容
5. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.(1)求证:BE=CE;
(2)若AB=6,∠BAC=54°,求$\widehat{AD}$的长.
分析 (1)如图,连接AE,利用圆周角定理推知AE是等腰△ABC的垂线,结合等腰三角形的性质证得结论;
(2)如图,连接OD,利用等腰三角形的性质和三角形内角和定理可以求得圆心角∠AOD的度数,然后利用弧长公式进行解答.
解答 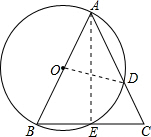 (1)证明:如图,连接AE.
(1)证明:如图,连接AE.
∵AB是圆O的直径,
∴∠AEB=90°,
即AE⊥BC.
又∵AB=AC,
∴AE是边BC上的中线,
∴BE=CE;
(2)解:∵AB=6,
∴OA=3.
又∵OA=OD,∠BAC=54°,
∴∠AOD=180°-2×54°=72°,
∴$\widehat{AD}$的长为:$\frac{72×π×3}{180}$=$\frac{6π}{5}$.
点评 本题考查了圆周角定理、弧长的计算以及等腰三角形的判定与性质.通过作辅助线,利用圆周角定理(或圆半径相等)的性质求得相关角的度数是解题的难点.

练习册系列答案
相关题目
15.在一次中学生田径运动会上,参加跳高的15名运动员的成绩如表所示:
那么这些运动员跳高成绩的众数和中位数分别是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
| A. | 3,2.5 | B. | 1.65,1.65 | C. | 1.65,1.70 | D. | 1.65,1.75 |
17.$\sqrt{64}$的立方根是( )
| A. | 2 | B. | ±2 | C. | 4 | D. | ±4 |
 已知:如图,在矩形ABCD中,E为AD的中点,连接BE、BD,过点A作AF⊥BE交BE于点F,连接FD.
已知:如图,在矩形ABCD中,E为AD的中点,连接BE、BD,过点A作AF⊥BE交BE于点F,连接FD. 如图是一个由7个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由7个相同的正方体组成的立体图形,它的主视图是( )



 如图,已知∠A=∠AEC=∠C=120°,试说明AB∥CD.
如图,已知∠A=∠AEC=∠C=120°,试说明AB∥CD. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=$\frac{1}{2}$AC•BD,其中正确的结论有( )
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=$\frac{1}{2}$AC•BD,其中正确的结论有( )