题目内容
16. 已知:如图,在矩形ABCD中,E为AD的中点,连接BE、BD,过点A作AF⊥BE交BE于点F,连接FD.
已知:如图,在矩形ABCD中,E为AD的中点,连接BE、BD,过点A作AF⊥BE交BE于点F,连接FD.(1)求证:△EAF∽△EBA;
(2)若AB=6,BC=8.求DF的长.
分析 (1)根据两角对应相等的两个三角形全等即可证明.
(2)作FM⊥AD于M,先利用勾股定理求出BE,利用$\frac{1}{2}$•AB•AE=$\frac{1}{2}$•BE•AF,求出AF,再利用勾股定理求出EF,根据$\frac{1}{2}$•AF•EF=$\frac{1}{2}$•AE•FM,求出FM,利用勾股定理求出AM,由此即可解决问题.
解答 (1)证明: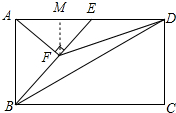 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AF⊥BE,
∴∠AFE=∠EAB=90°,
∵∠AEF=∠AEB,
∴△EAF∽△EBA.
(2)解:作FM⊥AD于M,
∵AB=6,AD=8,AE=ED,
∴AE=ED=4,
在RT△ABE中,BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,
∵$\frac{1}{2}$•AB•AE=$\frac{1}{2}$•BE•AF,
∴AF=$\frac{12\sqrt{13}}{13}$,
∴EF=$\sqrt{A{E}^{2}-A{F}^{2}}$=$\sqrt{{4}^{2}-(\frac{12\sqrt{13}}{13})^{2}}$=$\frac{8\sqrt{13}}{13}$.
∵$\frac{1}{2}$•AF•EF=$\frac{1}{2}$•AE•FM,
∴FM=$\frac{24}{13}$,AM=$\sqrt{A{F}^{2}-F{M}^{2}}$=$\frac{36}{13}$,
∴DM=AD-AM=$\frac{68}{13}$,
∴DF=$\sqrt{F{M}^{2}+D{M}^{2}}$=$\sqrt{(\frac{24}{13})^{2}+(\frac{68}{13})^{2}}$=$\frac{20\sqrt{13}}{13}$.
点评 本题考查相似三角形的性质和判定、勾股定理、矩形的性质等知识,解题的关键是学会利用面积法求高,属于中考常考题型.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 如图是由5个相同的正方体组成的立体图形,它的主视图是( )
如图是由5个相同的正方体组成的立体图形,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
表一:
| 试验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 针尖朝上次数 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 5 |
| 试验次数 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 针尖朝上次数 | 6 | 13 | 18 | 25 | 34 | 40 | 45 | 52 | 58 | 65 |
(2)求针尖朝上的概率估计值,并说明理由.
| A. | x2+x-6=0 | B. | x2-x-6=0 | C. | x2+6x-1=0 | D. | x2-6x+1=0 |

 如图,反比例函数y=$\frac{2}{x}$的图象与一次函数y=kx+b的图象交于点A、B,点A、B的横坐标分别为1,-2,一次函数图象与y轴的交于点C,与x轴交于点D.
如图,反比例函数y=$\frac{2}{x}$的图象与一次函数y=kx+b的图象交于点A、B,点A、B的横坐标分别为1,-2,一次函数图象与y轴的交于点C,与x轴交于点D. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.