题目内容
20.先化简,再求代数式($\frac{1}{x+y}$-$\frac{1}{{x}^{2}+xy}$)÷$\frac{x-1}{x}$的值,其中x=3,y=1.分析 先算括号里面的,再算除法,最后把x、y的值代入进行计算即可.
解答 解:原式=[$\frac{1}{x+y}$-$\frac{1}{x(x+y)}$]•$\frac{x}{x-1}$
=$\frac{x-1}{x(x+y)}$•$\frac{x}{x-1}$
=$\frac{1}{x+y}$,
当x=3,y=1时,原式=$\frac{1}{3+1}$=$\frac{1}{4}$.
点评 本题考查的是分式的化简求值,在解答此类问题时要注意分式要化为最简形式,以简化计算.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
10.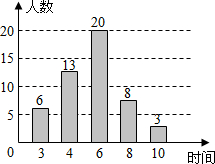 小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
 小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )| A. | 6,4 | B. | 6,6 | C. | 4,4 | D. | 4,6 |
8.小明和小杰为了估计抛掷图钉时针尖朝上的概率,分别做了试验.小明的试验结果记录在表一,小杰的试验结果记录在表二.
表一:
表二:
(1)在小明的试验中,针尖朝上的频率是多少?在小杰的试验中,针尖朝上的频率又是多少?
(2)求针尖朝上的概率估计值,并说明理由.
表一:
| 试验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 针尖朝上次数 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 5 |
| 试验次数 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 针尖朝上次数 | 6 | 13 | 18 | 25 | 34 | 40 | 45 | 52 | 58 | 65 |
(2)求针尖朝上的概率估计值,并说明理由.
12. 如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
 如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
10.已知实数a<0,则下列事件中是必然事件的是( )
| A. | 3a>0 | B. | a-3<0 | C. | a+3<0 | D. | a3>0 |

 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.