题目内容
5.解方程组:①$\left\{\begin{array}{l}{x+y=-1}\\{4x+y=5}\end{array}\right.$
②$\left\{\begin{array}{l}{y=x+1}\\{3x-2y=-5}\end{array}\right.$.
分析 ①方程组利用加减消元法求出解即可;
②方程组利用代入消元法求出解即可.
解答 解:①$\left\{\begin{array}{l}{x+y=-1①}\\{4x+y=5②}\end{array}\right.$,
②-①得:3x=6,即x=2,
把x=2代入①得:y=-3,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$;
②$\left\{\begin{array}{l}{y=x+1①}\\{3x-2y=-5②}\end{array}\right.$,
把①代入②得:3x-2x-2=-5,即x=-3,
把x=-3代入①得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
15.在平面直角坐标系中,到x轴的距离等于2个单位长度,且到y轴的距离等于3个单位长度的点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列从左到右的变形中是因式分解的是( )
| A. | (x+y)2=x2+2xy+y2 | B. | x2-5x+6=(x-2)(x-3) | ||
| C. | m2+m-3=m(m+1)-3 | D. | 5x2-3xy+x=x(5x-3y) |
14.等边三角形的边长为4,则该三角形的面积为( )
| A. | 4$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
15.下列函数中,y是x的一次函数的是( )
| A. | y=x2+2x | B. | y=-$\frac{8}{x}$ | C. | y=x | D. | y=$\sqrt{2x}$ |
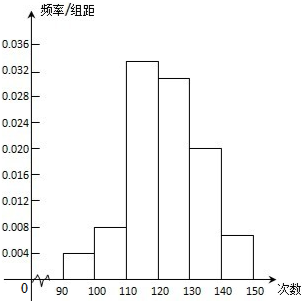 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.