题目内容
14.请你写出一条经过原点的抛物线的表达式y=x2+x(答案不惟一).分析 图象经过原点,要求解析式中,当x=0时,y=0,只要二次函数解析式常数项为0即可.
解答 解:依题意,二次函数的图象经过原点,
函数解析式的常数项为0,如y=x2+x(答案不惟一).
故答案为:y=x2+x(答案不惟一).
点评 本题考查了二次函数解析式与图象的位置关系.抛物线y=ax2+bx+c中,当b=0时,抛物线的对称轴为y轴,当c=0时,抛物线经过原点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列说法正确的是( )
| A. | 1既是素数又是合数 | B. | 两个不同的素数一定互素 | ||
| C. | 两个合数一定不互素 | D. | 两个奇数的公因数一定是1 |
2.计算:
(1)2$\sqrt{18}$-3$\sqrt{2}$-$\sqrt{\frac{1}{2}}$
(2)(3+$\sqrt{5}$)2-(2-$\sqrt{5}$)(2+$\sqrt{5}$)
(1)2$\sqrt{18}$-3$\sqrt{2}$-$\sqrt{\frac{1}{2}}$
(2)(3+$\sqrt{5}$)2-(2-$\sqrt{5}$)(2+$\sqrt{5}$)
9.(-8)2的立方根是( )
| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
4.多项式-$\frac{1}{5}$x|m|+(m-2)x+1是关于x的二次三项式,则m的值是( )
| A. | 2 | B. | -2 | C. | -4 | D. | 2或-2 |
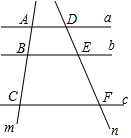 如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.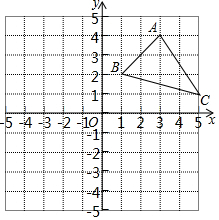 如图,在平面直角坐标系xOy中,有△ABC,请按要求完成下列各问题:
如图,在平面直角坐标系xOy中,有△ABC,请按要求完成下列各问题: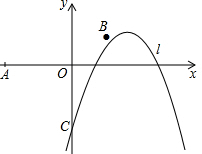 如图,已知点O (0,0),A (-5,0),B (2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.
如图,已知点O (0,0),A (-5,0),B (2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.