题目内容
19．在一个不透明的口袋中，有标有数字2，3，4除标号外其余均相同的3个小球，从袋中随机地摸取一个小球后然后放回，再随机地摸取一个小球，则两次摸取的小球标号之和为5的概率是$\frac{2}{9}$．分析 列表得出所有可能的情况数，找出之和为5的情况数，即可求出所求的概率．
解答 解：列表如下：
| 2 | 3 | 4 | |
| 2 | （2，2） | （3，2） | （4，2） |
| 3 | （2，3） | （3，3） | （4，3） |
| 4 | （2，4） | （3，4） | （4，4） |
则P之和为5=$\frac{2}{9}$．
故答案为：$\frac{2}{9}$．
点评 此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
计算高手系列答案
相关题目
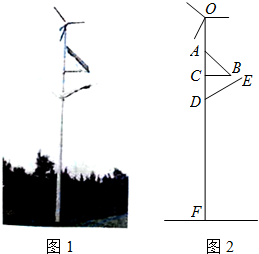如图1，某利用风能、太阳能发电的风光互补环保路灯的灯杆顶端装有风力发电机，中间装有太阳能板，下端装有路灯．该系统工作过程中某一时刻的截面图如图2，已知太阳能板的支架BC垂直于灯杆OF，路灯顶端E距离地面6米，DE=1.8米，∠CDE=60°．且根据我市的地理位置设定太阳能板AB的倾斜角为43°，AB=1.5米，CD=1米．为保证长为1米的风力发电机叶片无障碍安全旋转，叶片与太阳能板顶端A的最近距离不少于0.5米，求灯杆OF至少要多高（利用科学计算器可求得sin43°≈0.6820，cos43°≈0.7314，tan43°≈0.9325，结果保留两位小数）？
7．已知圆锥底面半径为2，母线长为5，则此圆锥侧面展开图的面积是（ ）
| A． | 5π | B． | 10π | C． | 7π | D． | 20π |
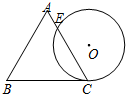如图，一个边长为4cm的等边三角形的高与ABC与⊙O直径相等，⊙O与BC相切于点C，⊙O与AC相交于点E，则CE的长为3cm．
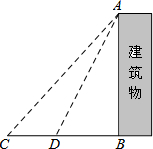某中学九年级数学兴趣小组想测量建筑物AB的高度．他们在C处仰望建筑物顶端，测得仰角为48°，再往建筑物的方向前进6米到达D处，测得仰角为64°，求建筑物的高度．（测角器的高度忽略不计，结果精确到0.1米）
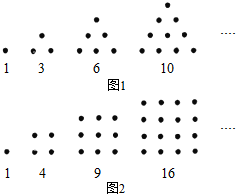古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数，比如：他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…，这样的数位正方形数（四边形数）．