Question

11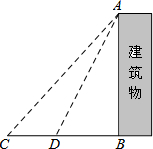．某中学九年级数学兴趣小组想测量建筑物AB的高度．他们在C处仰望建筑物顶端，测得仰角为48°，再往建筑物的方向前进6米到达D处，测得仰角为64°，求建筑物的高度．（测角器的高度忽略不计，结果精确到0.1米）
（参考数据：sin48°≈$\frac{7}{10}$，tan48°≈$\frac{11}{10}$，sin64°≈$\frac{9}{10}$，tan64°≈2）

Answer 1

分析 Rt△ADB中用AB表示出BD、Rt△ACB中用AB表示出BC，根据CD=BC-BD可得关于AB 的方程，解方程可得．

解答 解：根据题意，得∠ADB=64°，∠ACB=48°
在Rt△ADB中，tan64°=$\frac{AB}{BD}$，
则BD=$\frac{AB}{tan64°}$≈$\frac{1}{2}$AB，
在Rt△ACB中，tan48°=$\frac{AB}{CB}$，
则CB=$\frac{AB}{tan48°}$≈$\frac{10}{11}$AB，
∴CD=BC-BD
即6=$\frac{10}{11}$AB-$\frac{1}{2}$AB
解得：AB=$\frac{132}{9}$≈14.7（米），
∴建筑物的高度约为14.7米．

点评 本题考查解直角三角形的应用-仰角俯角问题，解题的关键是利用数形结合的思想找出各边之间的关系，然后找出所求问题需要的条件．