题目内容
13.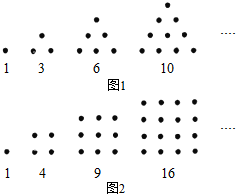 古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数位正方形数(四边形数).
古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数位正方形数(四边形数).(1)请你写出既是三角形数又是正方形数且大于1的最小正整数为36;
(2)试证明:当k为正整数时,k(k+1)(k+2)(k+3)+1必须为正方形数;
(3)记第n个k变形数位N(n,k)(k≥3).例如N(1,3)=1,N(2,3)=3,N(2,4)=4.
①试直接写出N(n,3)N(n,4)的表达式;
②通过进一步的研究发现N(n,5)=$\frac{3}{2}$n2-$\frac{1}{2}$n,N(n,6)=2n2-n,…,请你推测N(n,k)(k≥3)的表达式,并由此计算N(10,24)的值.
分析 (1)图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即$\frac{n(n+1)}{2}$;图2中1、4、9、16,…,第n个图中点的个数是n2,求出能同时满足两个式子的数,即可得出结果;
(2)通过因式分解,将k(k+1)(k+2)(k+3)+1化解为完全平方数,即为正方形数;
(3)①由图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即$\frac{n(n+1)}{2}$;图2中1、4、9、16,…,第n个图中点的个数是n2,即可得出结果;
②由N(n,3)=$\frac{(3-2){n}^{2}+(4-3)n}{2}$,N(n,4)=$\frac{(4-2){n}^{2}+(4-4)n}{2}$,N(n,5)=$\frac{(5-2){n}^{2}+(4-5)n}{2}$,N(n,6)=$\frac{(6-2){n}^{2}+(4-6)n}{2}$,可推断N(n,k)=$\frac{(k-2){n}^{2}+(4-k)n}{2}$(k≥3),将N(10,24)代入即可得出结果.
解答 (1)解:∵正方形数点的个数是为n2,∴除1外,分别为4,9,16,25,36,49,64,…,
∵图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即三角形数点的个数是为$\frac{n(n+1)}{2}$,
∵4=$\frac{n(n+1)}{2}$无正整数解,∴4不是三角形数,
∵9=$\frac{n(n+1)}{2}$无正整数解,∴9不是三角形数,
∵16=$\frac{n(n+1)}{2}$无正整数解,∴16不是三角形数,
∵25=$\frac{n(n+1)}{2}$无正整数解,∴25不是三角形数,
∵36=$\frac{n(n+1)}{2}$,解得n=8,所以36是三角形数,
∴除1外,最小的既是三角形数又是正方形数的是36,
故答案为36;
(2)证明:∵k(k+1)(k+2)(k+3)+1
=k(k+3)(k+1)(k+2)+1
=(k2+3k)(k2+3k+2)+1
=(k2+3k)2+2(k2+3k)+1
=(k2+3k+1)2
∴k(k+1)(k+2)(k+3)+1是完全平方数,即为正方形数;
(3)解:①由(1)知:N(n,3)=$\frac{n(n+1)}{2}$,N(n,4)=n2;
②∵N(n,3)=$\frac{n(n+1)}{2}$=$\frac{{n}^{2}+n}{2}$=$\frac{(3-2){n}^{2}+(4-3)n}{2}$,
N(n,4)=n2=$\frac{2{n}^{2}+0×n}{2}$=$\frac{(4-2){n}^{2}+(4-4)n}{2}$,
N(n,5)=$\frac{3}{2}$n2-$\frac{1}{2}$n=$\frac{3{n}^{2}-n}{2}$=$\frac{(5-2){n}^{2}+(4-5)n}{2}$,
N(n,6)=2n2-n=$\frac{4{n}^{2}-2n}{2}$=$\frac{(6-2){n}^{2}+(4-6)n}{2}$,
∴由此变化规律可推断N(n,k)=$\frac{(k-2){n}^{2}+(4-k)n}{2}$(k≥3);
∴N(10,24)=$\frac{(24-2)×1{0}^{2}+(4-24)×10}{2}$=1000.
点评 本题考查三角形数、正方形数的规律、完全平方数与归纳推理等知识,观察已知式子的规律并改写形式是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案| 姓名 | A | B | C | D | E | F | G | H | I |
| 成绩(米) | 0.91 | 0.95 | 1.10 | 0.98 | 1.08 | 0.96 | 1.12 | 1.18 | 1.17 |
(2)分别求出这组数据的平均数和中位数.
(3)你认为哪个数据代表这组数据的一般水平更合适?
(4)如果再增加一个同学的成绩是1.15米,这组数据的中位数是多少?
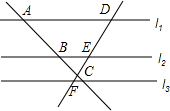 如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$=$\frac{2}{5}$.
如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$=$\frac{2}{5}$.