Question

1．在平面直角坐标系中，已知：点A（0，4），B（3，1），C（x，y）
（1）若BC的连线段平行于OA，且BC=2，①求x，y的值；②三角形ABC的面积；
（2）如果点C在x轴上，且以A、B、C三点为顶点的三角形的面积为9，求点C的坐标．

Answer 1

分析 （1）①由平行线的性质和点的坐标性质得出点C与B的横坐标相同，再由BC的长，得出点C的坐标即可；
②由三角形面积公式即可得出结果，注意分类讨论；
（2）设点C的坐标为（x，0），分两种情况：①点C在x轴的正半轴时，由三角形的面积得出方程，解方程即可；
②点C在x轴的负半轴时，由三角形的面积得出方程，解方程即可．

解答 解：（1）①∵BC∥OA，
∴点C与B的横坐标相同为3，
∵BC=2，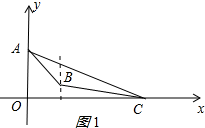
∴点C的纵坐标为-1或3；
∴x=3，y=-1或3；
②△ABC的面积=$\frac{1}{2}$×2×2=2；
（2）设点C的坐标为（x，0），分两种情况：
①点C在x轴的正半轴时，如图1所示：
△ABC的面积=$\frac{1}{2}$•4•x-$\frac{1}{2}$（4+1）×3-$\frac{1}{2}$（x-3）×1=9，
解得：x=10，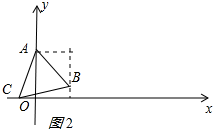
∴点C的坐标为（10，0）；
②点C在x轴的负半轴时，如图2所示：
△ABC的面积=3×4+$\frac{1}{2}$×4×（-x）-$\frac{1}{2}$（3-x）×1-$\frac{1}{2}$×3×3=9，
解得：x=-2，
∴点C的坐标为（-2，0）；
综上所述：点C的坐标为（10，0）或（-2，0）．

点评 本题考查了坐标与图形性质的应用、三角形面积的计算；熟练掌握坐标与图形性质是解决问题的关键；注意分类讨论思想的应用．