题目内容
6.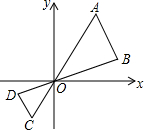 如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )
如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )| A. | (-2,-3) | B. | (-3,-2) | C. | (-3,-1) | D. | (-2,-1) |
分析 利用位似图形的性质结合两图形的位似比进而得出C点坐标.
解答 解:∵线段AB的两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,
∴端点C的横坐标和纵坐标都变为A点的一半的相反数,
∴端点C的坐标为:(-2,-3).
故选:A.
点评 此题主要考查了位似图形的性质,利用两图形的位似比得出对应点横纵坐标关系是解题关键.

练习册系列答案
相关题目
17.亮亮和晶晶掷一枚均匀的硬币,硬币落下后会出现两种情况,他们把结果制成表格:
(1)完成表格;
(2)根据表格,画出正面朝上的概率的折线统计图;
(3)观察你画出的折线统计图,你发现了什么规律?
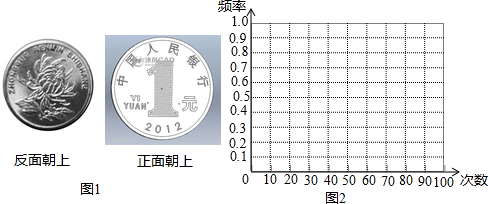
| 实验次数n | 10 | 20 | 30 | 40 | 50 | 60 | 80 | 100 |
| 正面朝上的次数m | 7 | 12 | 15 | 18 | 27 | 27 | 44 | 49 |
| 正面朝上的频率$\frac{m}{n}$ | 0.7 | 0.6 | 0.5 | 0.45 | 0.54 | 0.45 | 0.55 | 0.49 |
| 反面朝上的次数p | 3 | 8 | 15 | 22 | 23 | 33 | 36 | 51 |
| 反面朝上的频率$\frac{p}{n}$ | 0.3 | 0.4 | 0.5 | 0.55 | 0.46 | 0.55 | 0.45 | 0.51 |
(2)根据表格,画出正面朝上的概率的折线统计图;
(3)观察你画出的折线统计图,你发现了什么规律?

1.已知点A在双曲线y=-$\frac{4}{x}$上,点B在直线y=x-4上,且A、B两点关于y轴对称,设点A的坐标为(m,n),则$\frac{m}{n}$+$\frac{n}{m}$的值是( )
| A. | -6 | B. | -4 | C. | 6 | D. | 4 |
18.下列图形的三视图中,主视图和左视图不一样的是( )
| A. |  球 | B. |  圆锥 | C. |  圆柱 | D. |  长方体 |
15.对于反比例函数y=$\frac{2}{x}$,下列四个结论正确的是( )
| A. | 图象经过点(2,2) | B. | y随x的增大而减小 | ||
| C. | 图象位于第一、三象限 | D. | 当x<1时,y的值都大于2 |
16.由一些正偶数连续排成的数表如表(表中下一行中数的个数是上一行中数的个数的2倍):
若规定坐标号(m,n)表示第m行从左向右第n个数,则(6,9)所表示的数是80;数2014的坐标号是(10,496).
| 第1行 | 2 |
| 第2行 | 4 6 |
| 第3行 | 8 10 12 14 |
| … | … |
 如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图,则构成这个几何体的体积是( )cm3.
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图,则构成这个几何体的体积是( )cm3.