题目内容
1.已知点A在双曲线y=-$\frac{4}{x}$上,点B在直线y=x-4上,且A、B两点关于y轴对称,设点A的坐标为(m,n),则$\frac{m}{n}$+$\frac{n}{m}$的值是( )| A. | -6 | B. | -4 | C. | 6 | D. | 4 |
分析 先根据A、B两点关于y轴对称用m、n表示出点B的坐标,再根据点A在双曲线y=-$\frac{4}{x}$上,点B在直线y=x-4上得出mn与m+n的值,代入代数式进行计算即可.
解答 解:∵点A的坐标为(m,n),A、B两点关于y轴对称,
∴B(-m,n),
∵点A在双曲线y=-$\frac{4}{x}$上,点B在直线y=x-4上,
∴n=-$\frac{4}{m}$,-m-4=n,即mn=-4,m+n=-4,
∴原式=$\frac{(m+n)^{2}-2mn}{mn}$=$\frac{16+8}{-4}$=-6.
故选:A.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
9.已知实数x、y同时满足三个条件:①x-y=2-m,②4x-3y=2+m,③x>y,那么实数m的取值范围是( )
| A. | m>-2 | B. | m<2 | C. | m<-2 | D. | m>2 |
16.在面积为60的?ABCD中,过点A作AE⊥直线BC于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为( )
| A. | 22+11$\sqrt{3}$ | B. | 22-11$\sqrt{3}$ | C. | 22+11$\sqrt{3}$或22-11$\sqrt{3}$ | D. | 22+11$\sqrt{3}$或2+$\sqrt{3}$ |
6.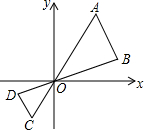 如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )
如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )
 如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )
如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )| A. | (-2,-3) | B. | (-3,-2) | C. | (-3,-1) | D. | (-2,-1) |
13.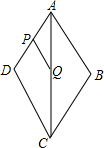 如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )
如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )
 如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )
如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )| A. | 6 | B. | 18$\sqrt{3}$ | C. | 24 | D. | 36$\sqrt{3}$ |
10.计算-2-3的结果是( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
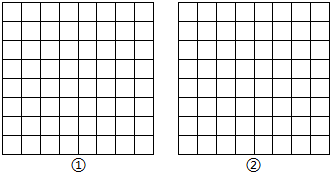 如图,正方形网格中的每一个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别在图①、图②中,画三角形和平行四边形.
如图,正方形网格中的每一个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别在图①、图②中,画三角形和平行四边形. 实数a和b在数轴上的对应点如图所示,化简:$\sqrt{{a}^{2}+4ab+4{b}^{2}}$+|a-b|.
实数a和b在数轴上的对应点如图所示,化简:$\sqrt{{a}^{2}+4ab+4{b}^{2}}$+|a-b|.