题目内容
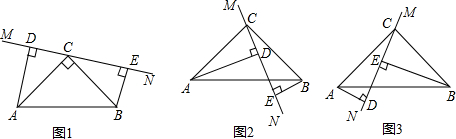
14.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系(不写证明过程);
(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系(不写证明过程).
分析 (1)利用垂直的定义得∠ADC=∠CEB=90°,则根据互余得∠DAC+∠ACD=90°,再根据等角的余角相等得到∠DAC=∠BCE,然后根据“AAS”可判断△ADC≌△CEB,所以CD=BE,AD=CE,再利用等量代换得到DE=AD+BE;
(2)与(1)一样可证明△ADC≌△CEB,则CD=BE,AD=CE,于是有DE=CE-CD=AD-BE;
(3)与(1)一样可证明△ADC≌△CEB,则CD=BE,AD=CE,于是有DE=CD-CE=BE-AD.
解答 (1)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠ECB}\\{AC=CB}\end{array}\right.$,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CE+CD=AD+BE;
(2)证明:与(1)一样可证明△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=CE-CD=AD-BE;
(3)解:DE=BE-AD.
点评 本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”,全等三角形的对应边相等,找准全等的三角形是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
9.已知实数x、y同时满足三个条件:①x-y=2-m,②4x-3y=2+m,③x>y,那么实数m的取值范围是( )
| A. | m>-2 | B. | m<2 | C. | m<-2 | D. | m>2 |
19.下列运算正确的是( )
| A. | a8÷a4=a2 | B. | (-3a3)2=6a6 | C. | a3+a5=a8 | D. | a-3•a4=a |
6.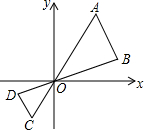 如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )
如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )
 如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )
如图,线段AB两个端点坐标分别为A(4,6),B(6,2),以原点O为位似中心,在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后,得到线段CD,则点C的坐标为( )| A. | (-2,-3) | B. | (-3,-2) | C. | (-3,-1) | D. | (-2,-1) |
3.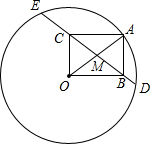 如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )
 如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )| A. | $\frac{24}{5}$ | B. | $\frac{28}{5}$ | C. | $\frac{36}{5}$ | D. | $\frac{48}{5}$ |
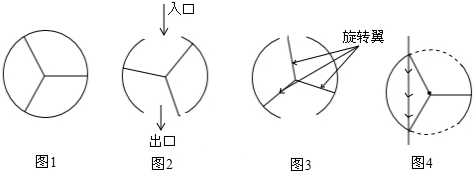
 如图,点O是线段AD、BC的中点,连接AB、CD,求证:∠B=∠C.
如图,点O是线段AD、BC的中点,连接AB、CD,求证:∠B=∠C. 如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明