题目内容
11．
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图，则构成这个几何体的体积是（ ）cm3．| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 根据俯视图可得出几何体的底层为4个小正方体，再结合主视图和左视图可得出上面是一个正方体，求体积即可．
解答 解：俯视图可得几何体的底层为4个小正方体，上层1个正方体，
共有5个正方体，
∵正方体的棱长为1cm，
∴正方体的体积为1cm3，
∴这个几何体的体积是5cm3，
故选C．
点评 本题考查了由三视图判断几何体，在已知三视图的情况下求几何体的体积，关键是还原得出实物图，再求体积．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
如图，点O是线段AD、BC的中点，连接AB、CD，求证：∠B=∠C．
19．下列运算正确的是（ ）
| A． | a8÷a4=a2 | B． | （-3a3）2=6a6 | C． | a3+a5=a8 | D． | a-3•a4=a |
6．
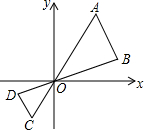如图，线段AB两个端点坐标分别为A（4，6），B（6，2），以原点O为位似中心，在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后，得到线段CD，则点C的坐标为（ ）
如图，线段AB两个端点坐标分别为A（4，6），B（6，2），以原点O为位似中心，在第三象限内将线段AB缩小为原来的$\frac{1}{2}$后，得到线段CD，则点C的坐标为（ ）| A． | （-2，-3） | B． | （-3，-2） | C． | （-3，-1） | D． | （-2，-1） |
16．太阳中心的温度是19200000℃，用科学记数法可将19200000℃表示为（ ）
| A． | 1.92×106 | B． | 19.2×106 | C． | 1.92×107 | D． | 0.192×107 |
3．
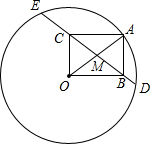如图，⊙O的半径为20，A是⊙O上一点．以OA为对角线作矩形OBAC，且OC=12．延长BC，与⊙O分别交于D，E两点，则CE-BD的值等于（ ）
如图，⊙O的半径为20，A是⊙O上一点．以OA为对角线作矩形OBAC，且OC=12．延长BC，与⊙O分别交于D，E两点，则CE-BD的值等于（ ）| A． | $\frac{24}{5}$ | B． | $\frac{28}{5}$ | C． | $\frac{36}{5}$ | D． | $\frac{48}{5}$ |
1．
如图，直线a∥b，直线c与a，b相交，∠1=50°，则∠2的度数为（ ）
如图，直线a∥b，直线c与a，b相交，∠1=50°，则∠2的度数为（ ）| A． | 40° | B． | 50° | C． | 120° | D． | 130° |