题目内容
先观察下列等式,再回答问题:
=1+
-
=1
;
=1+
-
=1
=1+
-
=1
(1)根据上面三个等式提供的信息,请你猜想
的结果,并进行验证;
(2)请按照上面各等式反映的规律,试用含n的式子表示出来;
(3)若S=
+
+
+…+
,求S.
1+
|
| 1 |
| 1 |
| 1 |
| 1+1 |
| 1 |
| 2 |
1+
|
| 1 |
| 2 |
| 1 |
| 2+1 |
| 1 |
| 6 |
1+
|
| 1 |
| 3 |
| 1 |
| 3+1 |
| 1 |
| 12 |
(1)根据上面三个等式提供的信息,请你猜想
1+
|
(2)请按照上面各等式反映的规律,试用含n的式子表示出来;
(3)若S=
1+
|
1+
|
1+
|
1+
|
考点:二次根式的性质与化简
专题:规律型
分析:(1)从三个式子中可以发现,第一个加数都是1,第二个加数是个分数,设分母为n,第三个分数的分母就是n+1,结果是一个带分数,整数部分是1,分数部分的分子也是1,分母是前项分数的分母的积.所以由此可计算给的式子;
(2)根据(1)找的规律写出表示这个规律的式子.;
(3)根据规律得出算式,最后求出即可.
(2)根据(1)找的规律写出表示这个规律的式子.;
(3)根据规律得出算式,最后求出即可.
解答:解:(1)
=1
,
理由是:
=
=
=
=1
;
(2)
=1+
-
=1+
;
(3)S=
+
+
+…+
=1+
+1+
+1+
+…+1+
=2013+1-
+
-
+
-
+…+
-
=2013+1-
=2013
.
1+
|
| 1 |
| 20 |
理由是:
1+
|
1+
|
|
| 21 |
| 20 |
| 1 |
| 20 |
(2)
1+
|
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n(n+1) |
(3)S=
1+
|
1+
|
1+
|
1+
|
=1+
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
=2013+1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2013 |
| 1 |
| 2014 |
=2013+1-
| 1 |
| 2014 |
=2013
| 2013 |
| 2014 |
点评:考查了二次根式的性质与化简,此题是一个阅读题目,通过阅读找出题目隐含条件.总结:找规律的题,都要通过仔细观察找出和数之间的关系,并用关系式表示出来.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形中,不是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,某拦河坝的横断面为梯形ABCD,若坝顶AD=3m,坝底BC=
如图,某拦河坝的横断面为梯形ABCD,若坝顶AD=3m,坝底BC=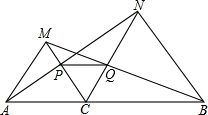 如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.
如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.