题目内容
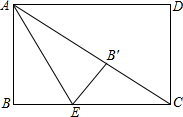 如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为
如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为考点:翻折变换(折叠问题),勾股定理
专题:
分析:利用勾股定理列式求出AC,根据翻折变换的性质可得AB′=AB,B′E=BE,然后求出B′C,设BE=x,表示出CE、BE′,然后利用勾股定理列方程求解即可.
解答:解:∵长方形ABCD中,AB=3,BC=4,
∴AC=
=
=5,
由翻折变换的性质得,AB′=AB=3,B′E=BE,
∴B′C=5-3=2,
设BE=x,则CE=4-x,BE′=x,
在Rt△B′CE中,由勾股定理得,B′E2+B′C2=CE2,
即x2+22=(4-x)2,
解得x=1.5,
即BE=1.5.
故答案为:1.5.
∴AC=
| AB2+BC2 |
| 32+42 |
由翻折变换的性质得,AB′=AB=3,B′E=BE,
∴B′C=5-3=2,
设BE=x,则CE=4-x,BE′=x,
在Rt△B′CE中,由勾股定理得,B′E2+B′C2=CE2,
即x2+22=(4-x)2,
解得x=1.5,
即BE=1.5.
故答案为:1.5.
点评:本题考查了翻折变换的性质,勾股定理,此类题目熟记性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
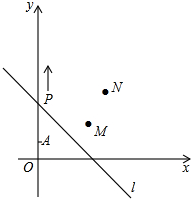 如图,A(0,2),M(4,3),N(5,6),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线L:y=-x+b也随之平移,设移动时间为t秒,若点M,N位于直线L的异侧,则t的取值范围是
如图,A(0,2),M(4,3),N(5,6),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线L:y=-x+b也随之平移,设移动时间为t秒,若点M,N位于直线L的异侧,则t的取值范围是 已知,如图,在△ABC中,AD=BD,∠BDE=∠DAC,求证:AE•BC=BD•AB.
已知,如图,在△ABC中,AD=BD,∠BDE=∠DAC,求证:AE•BC=BD•AB. 以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于D,过点D作⊙O的切线交BC于点E,连接OE.求证:EB=EC=ED.
以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于D,过点D作⊙O的切线交BC于点E,连接OE.求证:EB=EC=ED. 如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC分别交DE、BE于点G、H,则∠EFC=
如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC分别交DE、BE于点G、H,则∠EFC= 如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若∠PMO=33°,∠PNO=70°,则∠QPN的度数为
如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若∠PMO=33°,∠PNO=70°,则∠QPN的度数为