题目内容
已知函数y=ax2+bx+c,若a>0,b<0,c<0,问这个函数的图象与x轴交点情况.
考点:二次函数图象与系数的关系
专题:
分析:先根据根的判别式△=b2-4ac>0,即这个函数图象与x轴有两个交点,根据根与系数的关系可知x1•x2=
,由于a>0,c<0,所以x1•x2<0,x1、x2异号.
| c |
| a |
解答:解:∵△=b2-4ac>0,
∴这个函数图象与x轴有两个交点,
设这个函数图象与x轴两个交点的坐标为(x1,0)、(x2,0),
∵x1•x2=
,a>0,c<0,
∴x1•x2<0,
∴一个在x轴的正半轴,另一个在x轴的负半轴.
∴这个函数图象与x轴有两个交点,
设这个函数图象与x轴两个交点的坐标为(x1,0)、(x2,0),
∵x1•x2=
| c |
| a |
∴x1•x2<0,
∴一个在x轴的正半轴,另一个在x轴的负半轴.
点评:本题考查的是二次函数的图象与系数的关系、根的判别式及根与系数的关系,解答此类题目时能把一元二次方程根的情况与二次函数的图象相结合是解答此类题目的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
下列各式计算正确的是( )
| A、4m2n-2mn2=2mn |
| B、-2a+5b=3ab |
| C、4xy-3xy=xy |
| D、a2+a2=a4 |
下列学习用具中,不考虑尺具上的刻度文字,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
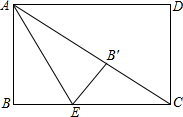 如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为
如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为