题目内容
 以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于D,过点D作⊙O的切线交BC于点E,连接OE.求证:EB=EC=ED.
以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于D,过点D作⊙O的切线交BC于点E,连接OE.求证:EB=EC=ED.考点:切线的性质
专题:证明题
分析:连接OD,根据切线的性质,由DE是⊙O的切线得到∠ODE=90°,再利用“HL”证明Rt△ODE≌Rt△OBE,得到ED=EB,∠1=∠2,由三角形外角性质得∠BOD=∠A+∠3,加上∠A=∠3,则∠2=∠4,于是可判断OE∥AC,利用点O为AB的中点,得到OE为△ABC的中位线,所以CE=EB,于是有EB=EC=ED.
解答:证明:连接OD,如图,
∵DE是⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
在Rt△ODE和Rt△OBE中,
,
∴Rt△ODE≌Rt△OBE(HL),
∴ED=EB,∠1=∠2,
∵∠BOD=∠A+∠3,
而OA=OD,
∴∠A=∠3,
∴∠2=∠4,
∴OE∥AC,
而点O为AB的中点,
∴OE为△ABC的中位线,
∴CE=EB,
∴EB=EC=ED.

∵DE是⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
在Rt△ODE和Rt△OBE中,
|
∴Rt△ODE≌Rt△OBE(HL),
∴ED=EB,∠1=∠2,
∵∠BOD=∠A+∠3,
而OA=OD,
∴∠A=∠3,
∴∠2=∠4,
∴OE∥AC,
而点O为AB的中点,
∴OE为△ABC的中位线,
∴CE=EB,
∴EB=EC=ED.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
22600000000用科学记数法表示为( )
| A、22.6×1010 |
| B、2.26×1011 |
| C、2.26×1010 |
| D、226×108 |
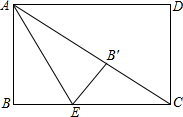 如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为
如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为 已知四边形ABCD的面积为4,∠ADC=∠B=90°,AD=DC,求点D到AB的距离DF.
已知四边形ABCD的面积为4,∠ADC=∠B=90°,AD=DC,求点D到AB的距离DF. 如图所示,直线AB、CD相交于点O,OE是∠AOD的平分线,∠FOC=90°,∠1=70°,求∠2与∠3的度数.
如图所示,直线AB、CD相交于点O,OE是∠AOD的平分线,∠FOC=90°,∠1=70°,求∠2与∠3的度数.