题目内容
 已知,如图,在△ABC中,AD=BD,∠BDE=∠DAC,求证:AE•BC=BD•AB.
已知,如图,在△ABC中,AD=BD,∠BDE=∠DAC,求证:AE•BC=BD•AB.考点:相似三角形的判定与性质
专题:证明题
分析:证明∠EAD=∠B、∠AED=∠BAC,得到△AED∽△BAC,列出比例式即可解决问题.
解答: 证明:∵AD=BD,
证明:∵AD=BD,
∴∠EAD=∠B=α;
设∠BDE=∠DAC=β,
∴∠AED=α+β,而∠BAC=α+β,
∴∠AED=∠BAC,而∠EAD=∠B,
∴△AED∽△BAC,
∴
=
,而AD=BD,
∴AE•BC=BD•AB.
 证明:∵AD=BD,
证明:∵AD=BD,∴∠EAD=∠B=α;
设∠BDE=∠DAC=β,
∴∠AED=α+β,而∠BAC=α+β,
∴∠AED=∠BAC,而∠EAD=∠B,
∴△AED∽△BAC,
∴
| AE |
| AB |
| AD |
| BC |
∴AE•BC=BD•AB.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深刻把握题意,准确找出命题中隐含的等量关系,正确推理论证.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
下列学习用具中,不考虑尺具上的刻度文字,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
若一个三角形的三边为5,12,13,那么这个三角形的外接圆的半径是( )
| A、5 | B、6 | C、6.5 | D、不能确定 |
一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h=-5t2+10t+1,则小球距离地面的最大高度是( )
| A、1米 | B、5米 | C、6米 | D、7米 |
 已知,∠DAB=∠CAE,AD=2,AC=6,AE=4,AB=3,DE=5,求BC长.
已知,∠DAB=∠CAE,AD=2,AC=6,AE=4,AB=3,DE=5,求BC长.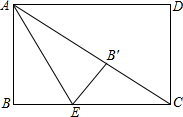 如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为
如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为 如图,AE∥BF∥CG∥DH,AB=
如图,AE∥BF∥CG∥DH,AB=